The gambler’s ruin problem

This is a classic probability problem equivalent to a simple random walk on the nonnegative integers. The set-up is that a gambler plays a game where on each play, they win one dollar with probability $p$ and lose one dollar with probability $1-p$. They keep playing until either they go broke or win $k$ dollars. What is the probability that they leave a winner?

The sample space in this problem is all possible sequences of plays. This is a big collection, and we won’t be able to resolve the probabilities of events by counting arguments. However, we do know, given that the gambler has $j$ dollars after some play, their possible fortune at the next play and the associated probabilities; this information can be used to resolve the problem.

Define $X_n$ to be the gambler’s fortune after $n$ plays, for $n=0,1,2,\dots$; $X_n=j$ defines the event that the gambler has $j$ dollars at play $n$, for each $j$ and $n$. The problem set-up is that for every $n,j$: $$P(X_{n+1}=x|X_n=j)=\{\begin{array}{ll}p,& x=j+1\\ 1-p,& x=j-1\end{array}$$

Now we are interested in the probability that the gambler wins $k$ dollars; denote this event by $W_k$. This will change over the course of play and depend on how much they have at any given time. So consider: $$a_j=P(W_k|X_n=j)\text{for each }j=0,\dots ,k$$

Note that $a_0=0$, since the gambler cannot win if they have no money left to play (i.e., $W_k\cap \{X_n=0\}=\mathrm{\varnothing }$ for every $n$), and $a_k=1$, since if the gambler has $k$ dollars they have won (i.e., $W_k\supset \{X_n=k\}$ for every $n$). Now, the probability of winning depends only on the most recent play; the plays before are irrelevant. Thus, $P(W_k|X_{n+1},X_n)=P(W_k|X_{n+1})$ (This is known as the Markov property.) Using the law of total (conditional) probability (see HW3 for a proof), we have that for each $j$: $$\begin{array}{rl}P(W_k|X_n=j)& =P(W_k|X_{n+1}=j+1)P(X_{n+1}=j+1|X_n=j)\\ & +P(W_k|X_{n+1}=j-1)P(X_{n+1}=j-1|X_n=j)\end{array}$$ And therefore $a_j=p{a}_{j+1}+(1-p)a_{j-1}$. Some rearrangement yields that: $$a_{j+1}-a_j=(a_j-a_{j-1})\left(\frac{1-p}{p}\right)$$

Since $a_0=0$, $a_2-a_1=a_1\left(\frac{1-p}{p}\right)$, and then by recursion we obtain: $$a_{j+1}-a_j=a_1{\left(\frac{1-p}{p}\right)}^{j}j=1,2,\dots ,k-1$$ Then by writing $a_{j+1}-a_1$ as a telescoping sum $\sum _{i=1}^j(a_{i+1}-a_i)$, we can express $a_{j+1}$ as a geometric series and obtian: $$a_{j+1}=\sum _{i=0}^j{a}_1{\left(\frac{1-p}{p}\right)}^i=\{\begin{array}{ll}{a}_1\left[\frac{1-{\left(\frac{1-p}{p}\right)}^{j+1}}{1-\left(\frac{1-p}{p}\right)}\right],& p\ne \frac{1}{2}\\ a_1(j+1),& p=\frac{1}{2}\end{array}$$ Then, using the fact that $a_k=1$, we get: $$a_1=\{\begin{array}{ll}\frac{1-\left(\frac{1-p}{p}\right)}{1-{\left(\frac{1-p}{p}\right)}^k},& p\ne \frac{1}{2}\\ \frac{1}{k},& p=\frac{1}{2}\end{array}$$ And finally, by substituting this into the expression above for $a_{j+1}$, we obtain for each $j=0,\dots ,k$: $$a_j=\{\begin{array}{ll}\frac{1-{\left(\frac{1-p}{p}\right)}^j}{1-{\left(\frac{1-p}{p}\right)}^k},& p\ne \frac{1}{2}\\ \frac{j}{k},& p=\frac{1}{2}\end{array}$$

We can use this to solve the problem. For instance, if the game is fair ($p=\frac{1}{2}$) and the gambler starts with $10, their probability of winning $100 is $P(W_{100}|X_n=10)=\frac{10}{100}=0.1$. If $p=\frac{2}{3}$, the same probability is: $$P(W_{100}|X_n=10)=\frac{1-\frac{1}{2^{10}}}{1-\frac{1}{2^{100}}}\approx 0.999$$

If the gambler could play forever, what is the probability of getting infinitely rich? Take the limit in $k$ to obtain: $$\underset{k\to \mathrm{\infty }}{lim}P(W_k|X_n=j)=\{\begin{array}{ll}0,& p\le \frac{1}{2}\\ 1-{\left(\frac{1-p}{p}\right)}^j,& p>\frac{1}{2}\end{array}$$

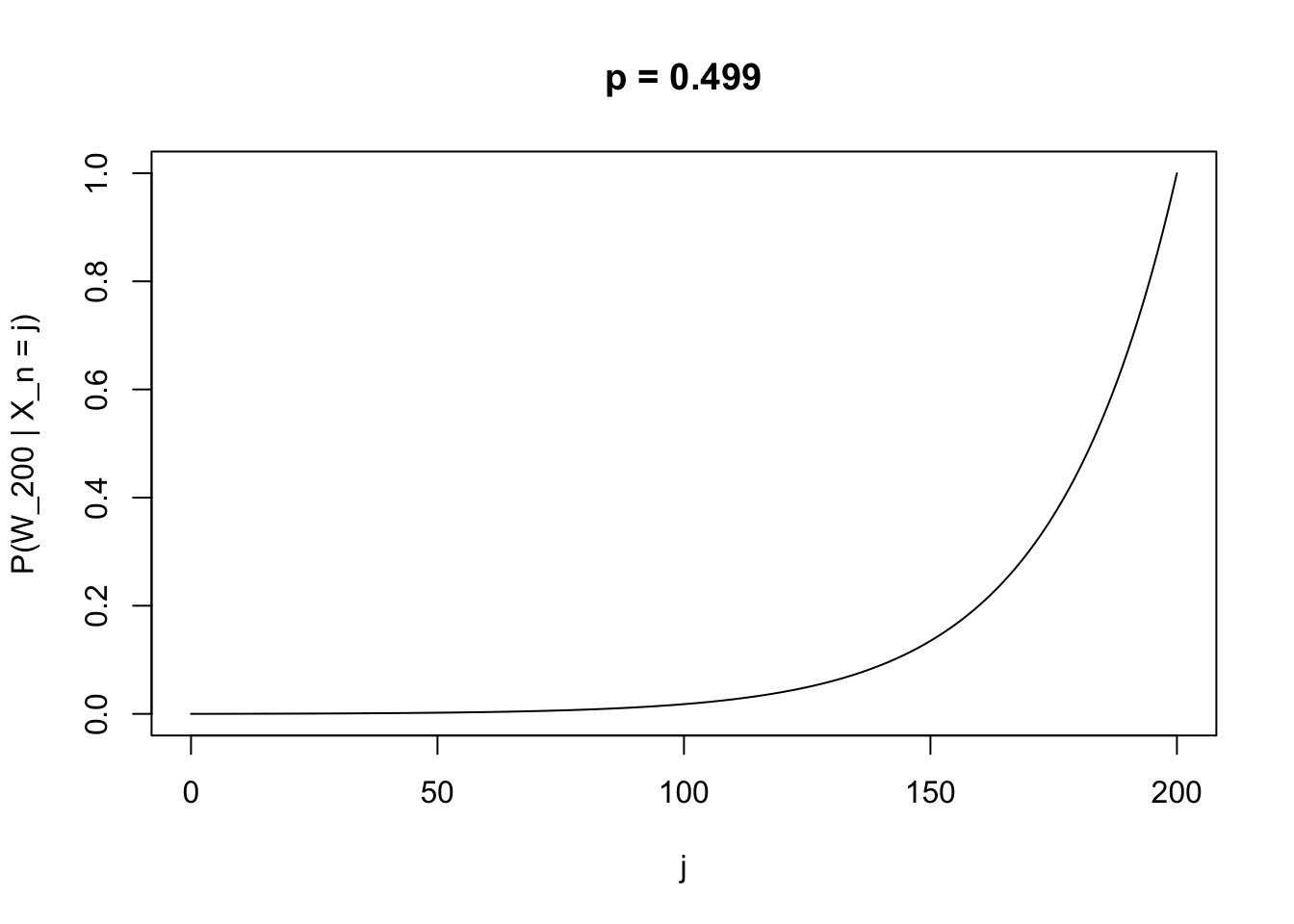
It’s actually somewhat interesting to plot the solution path in $j$ for various $p,k$. For instance, when $p=0.49$, and the game is only barely unfavorable, the probability of winning $200 is negligible until the gambler acquires most of the money they wish to win.

For an extension of the problem, consider finding the minimum $j$ such that $P(W_k|X_n=j)\ge \frac{1}{2}$ in terms of $p$, in other words, the smallest amount of money to start with that ensures favorable odds of winning, given $p$. Or, try plotting solution paths in $p$.