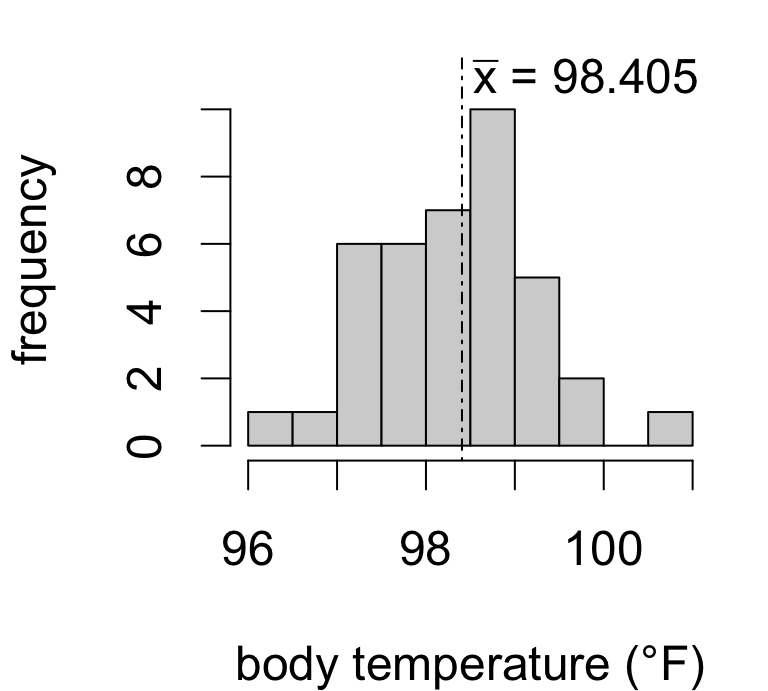
| mean | sd | n | se |
|---|---|---|---|
| 98.41 | 0.9162 | 39 | 0.1467 |
Applied Statistics for Life Sciences

| mean | sd | n | se |
|---|---|---|---|
| 98.41 | 0.9162 | 39 | 0.1467 |
Is the true mean body temperature actually 98.6°F?
Seems plausible given our data.
But what if the sample mean were instead…
| \(\bar{x}\) | consistent with \(\mu = 98.6\)? |
|---|---|
| 98.30 | probably still yes |
| 98.15 | maybe |
| 98.00 | hesitating |
| 97.85 | skeptical |
| 97.40 | unlikely |
Consider how many standard errors away from the hypothesized value we’d be:
| \(\bar{x}\) | estimation error | no. SE’s | interpretation |
|---|---|---|---|
| 98.30 | -0.3 | 2 | double the average error |
| 98.15 | -0.45 | 3 | triple the average error |
| 98.00 | -0.6 | 4 | quadruple |
| 97.85 | -0.75 | 5 | quintuple |
| 97.40 | -1.2 | 8 | octuple! |
We know from interval coverage that:
So if the estimation error exceeds 2-3SE, the data aren’t consistent with the hypothesis.
If we want to test the hypothesis
\[H_0: \mu = 98.6\]
against the alternative
\[H_A: \mu \neq 98.6\]
then we consider the test statistic
\[T = \frac{\bar{x} - 98.6}{s_x/\sqrt{n}} \qquad\left(\frac{\text{estimation error}}{\text{standard error}}\right)\]
Two possible outcomes:
\(\Longrightarrow\) the data are consistent with \(H_0\)
\(\Longrightarrow\) the data favor \(H_A\)
To formalize the test we just need to decide: how many SE’s is large enough to reject \(H_0\)?
If the population mean is in fact 98.6°F then \[T = \frac{\bar{x} - 98.6}{s_x/\sqrt{n}} \qquad\left(\frac{\text{estimation error}}{\text{standard error}}\right)\] has a sampling distribution that is well-approximated by a \(t_{39 - 1}\) model.
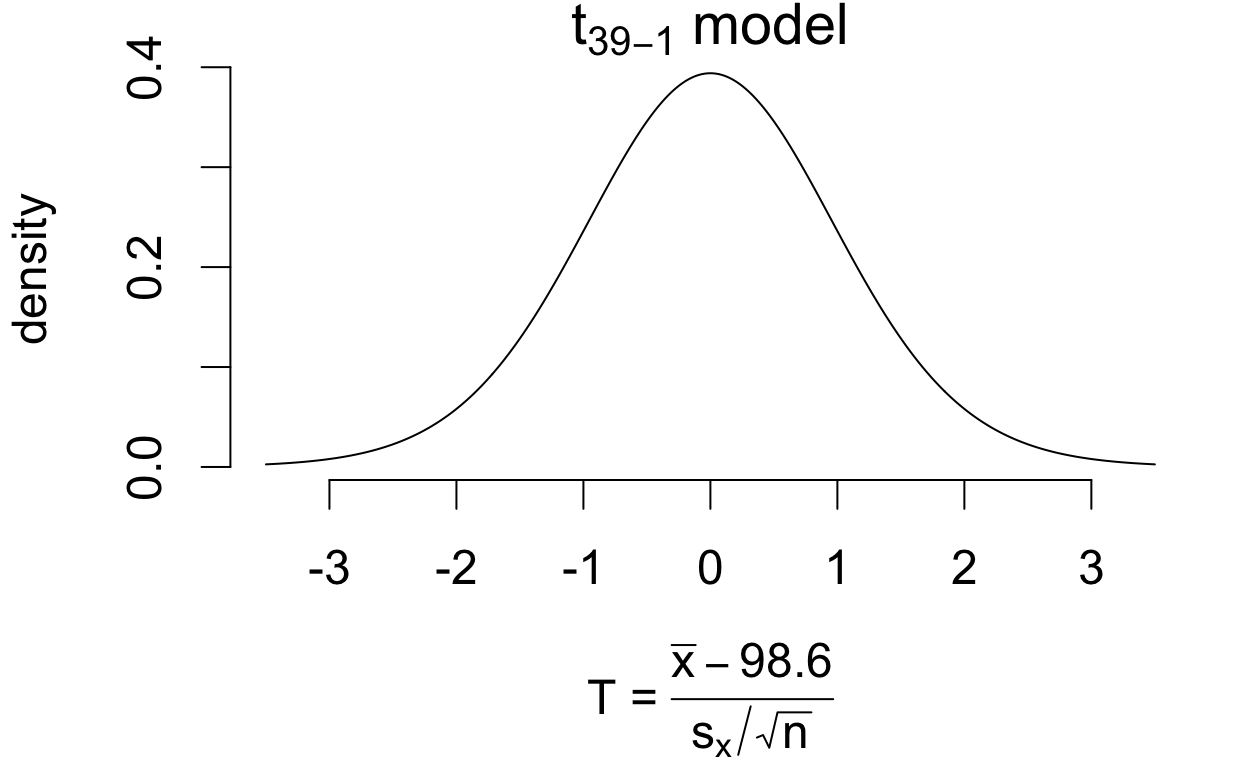
If the population mean is in fact 98.6°F then \[T = \frac{\bar{x} - 98.6}{s_x/\sqrt{n}}\qquad\left(\frac{\text{estimation error}}{\text{standard error}}\right)\] has a sampling distribution that is well-approximated by a \(t_{39 - 1}\) model.
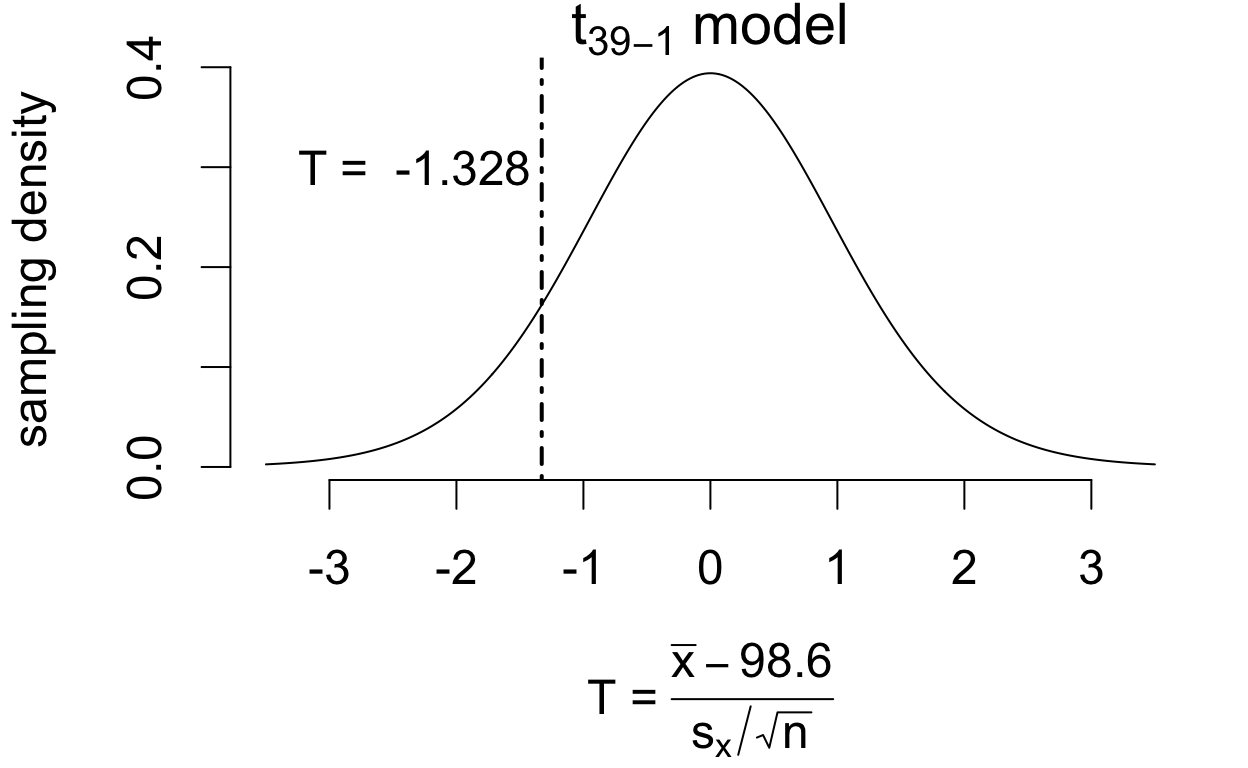
If the population mean is in fact 98.6°F then \[ T = \frac{\bar{x} - 98.6}{s_x/\sqrt{n}} \qquad\left(\frac{\text{estimation error}}{\text{standard error}}\right) \] has a sampling distribution that is well-approximated by a \(t_{39 - 1}\) model.
If the population mean is in fact 98.6°F then \[ T = \frac{\bar{x} - 98.6}{s_x/\sqrt{n}} \qquad\left(\frac{\text{estimation error}}{\text{standard error}}\right) \] has a sampling distribution that is well-approximated by a \(t_{39 - 1}\) model.
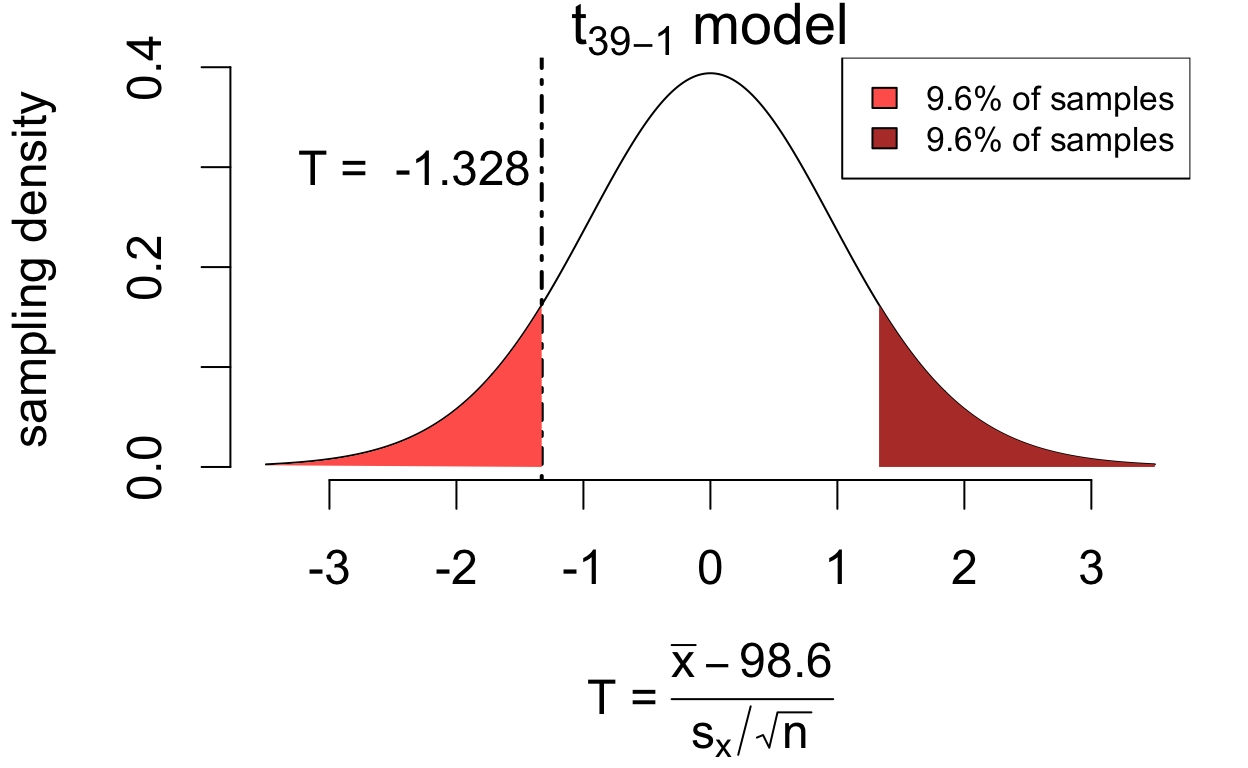
If the population mean is in fact 98.6°F then \[ T = \frac{\bar{x} - 98.6}{s_x/\sqrt{n}} \qquad\left(\frac{\text{estimation error}}{\text{standard error}}\right) \] has a sampling distribution that is well-approximated by a \(t_{39 - 1}\) model.
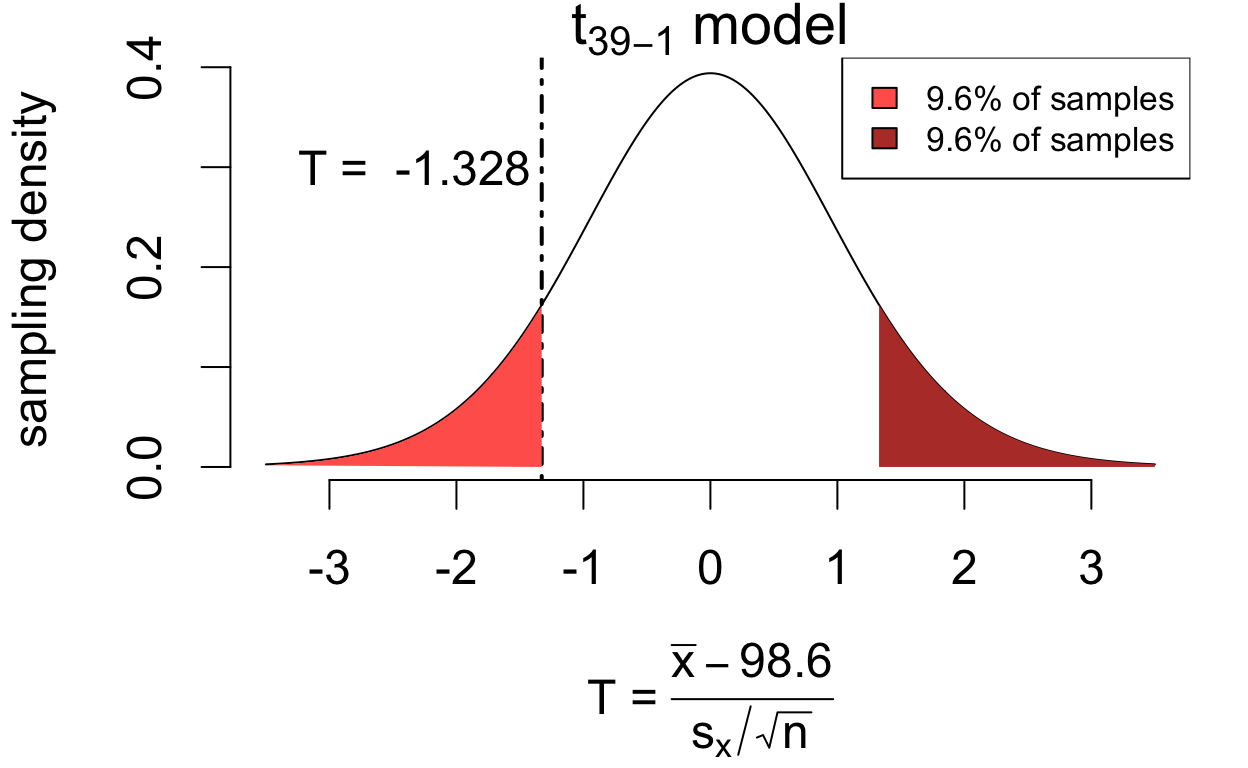
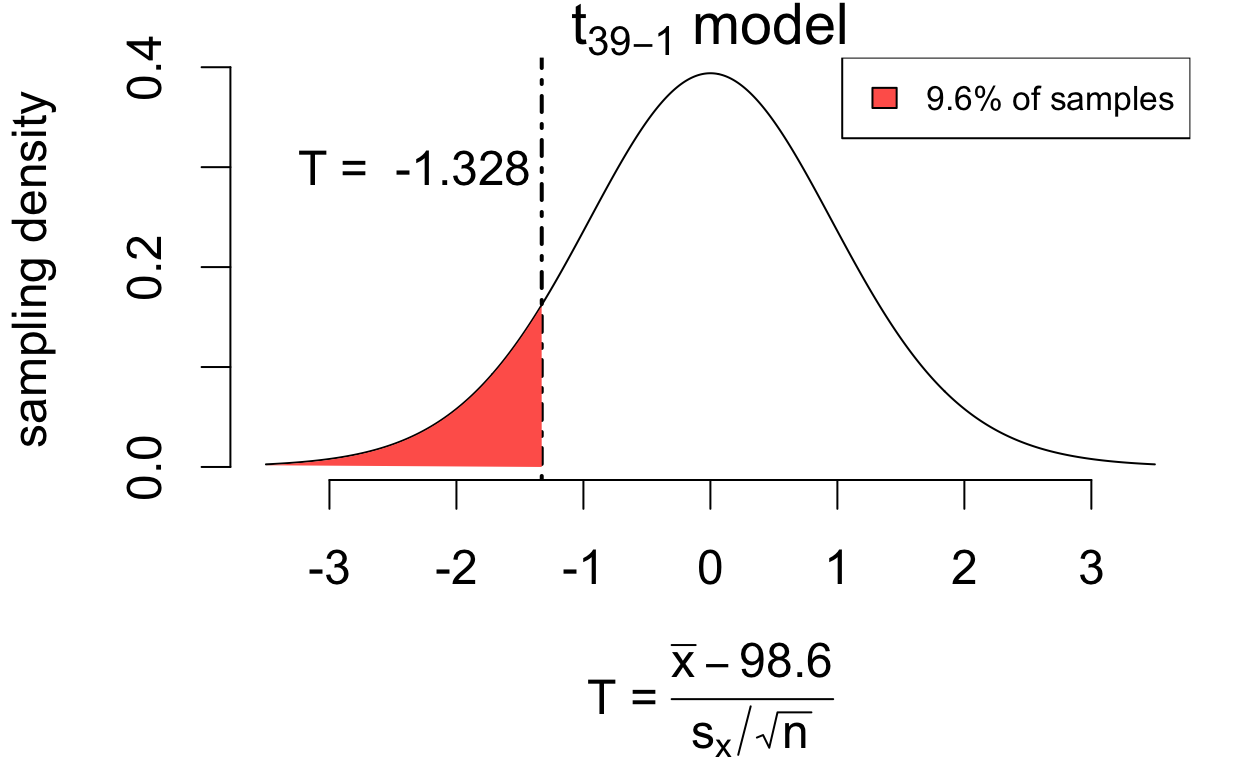
\[P(|T| > 1.328) = 0.192\]
If the hypothesis were true, we’d see at least as much estimation error 19.2% of the time. So the data are consistent with the hypothesis \(\mu = 98.6\).
If the population mean is in fact 98.6°F then \[ T = \frac{\bar{x} - 98.6}{s_x/\sqrt{n}} \qquad\left(\frac{\text{estimation error}}{\text{standard error}}\right) \] has a sampling distribution that is well-approximated by a \(t_{39 - 1}\) model.
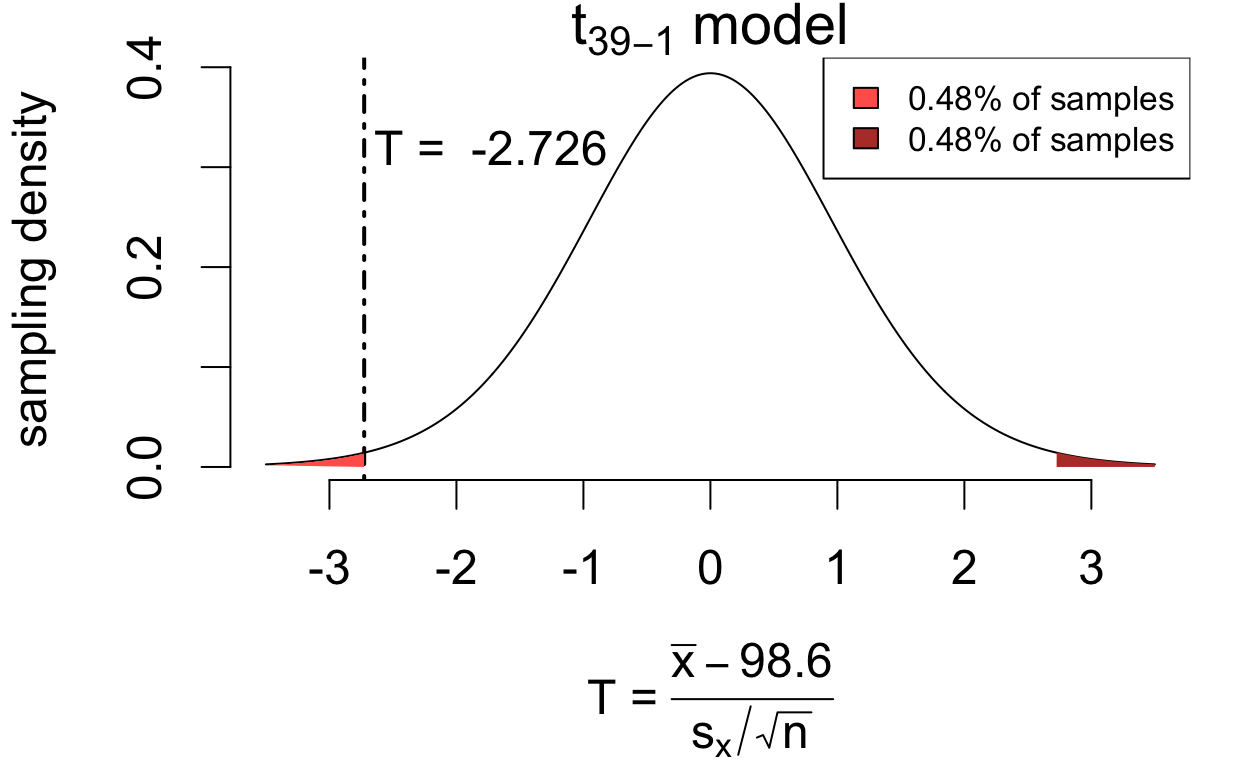
\[P(|T| > 2.726) = 0.0096\]
If the hypothesis were true, we’d see at least as much estimation error only 0.96% of the time. So the data are not consistent with the hypothesis \(\mu = 98.6\)
We just made these assessments:
| sample.mean | se | t.stat | how.often | evaluation |
|---|---|---|---|---|
| 98.41 | 0.1467 | -1.328 | 0.192 | not unusual |
| 98.2 | 0.1467 | -2.726 | 0.009632 | unusual |
The sampling frequency we’re calculating above is called a p-value: the proportion of samples for which the test statistic, under \(H_0\), would exceed the observed value.
The convention is to reject the hypothesis whenever p < 0.05. The threshold 0.05 is called the “significance level” or simply “level” of the test.
To test the hypotheses:
\[ \begin{cases} H_0: \mu = \mu_0\\ H_A: \mu \neq \mu_0 \end{cases} \]
Steps:
# point estimate and standard error
temp.mean <- mean(temps$body.temp)
temp.mean.se <- sd(temps$body.temp)/sqrt(nrow(temps))
# compute test statistic
tstat <- (temp.mean - 98.6)/temp.mean.se
tstat[1] -1.328265# proportion of samples where T exceeds observed value
p.val <- 2*pt(abs(tstat), df = 38, lower.tail = F)
p.val[1] 0.1920133[1] FALSEWe call this a \(t\)-test for the population mean. Interpretation in conventional style:
The data do not provide evidence that the mean body temperature differs from 98.6°F (T = -1.328 on 38 degrees of freedom, p = 0.192).
There are two ways to make a mistake in a hypothesis test – two “error types”.
| Reject \(H_0\) | Fail to reject \(H_0\) | |
|---|---|---|
| True \(H_0\) | type I error | correct decision |
| False \(H_0\) | correct decision | type II error |
The type I error rate is controlled at the significance level \(\alpha\) by design.
Type II error is trickier, because the sampling distribution of the test statistic depends on the value of the population mean under specific alternatives – we’ll revisit this later.
A hypothesis test boils down to deciding whether your estimate is too far from a hypothetical value for that hypothesis to be plausible.
To test the hypotheses:
\[ \begin{cases} H_0: &\mu = \mu_0 \\ H_A: &\mu \neq \mu_0 \end{cases} \]
We use the test statistic:
\[ T = \frac{\bar{x} - \mu_0}{SE(\bar{x})} \quad\left(\frac{\text{estimation error under } H_0}{\text{standard error}}\right) \]
We say \(H_0\) is implausible at level \(\alpha\) if:
This decision rule controls the type I error rate at level \(\alpha\).
Test the hypothesis that the average U.S. adult sleeps 8 hours.

| estimate | std.err | tstat | pval |
|---|---|---|---|
| 6.96 | 0.02 | -42.53 | <0.0001 |
95% confidence interval: (6.91, 7.01)
The data provide evidence that the average U.S. adult does not sleep 8 hours per night (T = -42.53 on 3178 degrees of freedom, p < 0.0001). With 95% confidence, the mean nightly hours of sleep among U.S. adults is estimated to be between 6.91 and 7.01 hours, with a point estimate of 6.59 hours (SE: 0.0245).
The test and interval convey complementary information:
A level \(\alpha\) test rejects \(H_0: \mu = \mu_0\) exactly when \(\mu_0\) is outside the \((1 - \alpha)\times 100\)% confidence interval for \(\mu\).
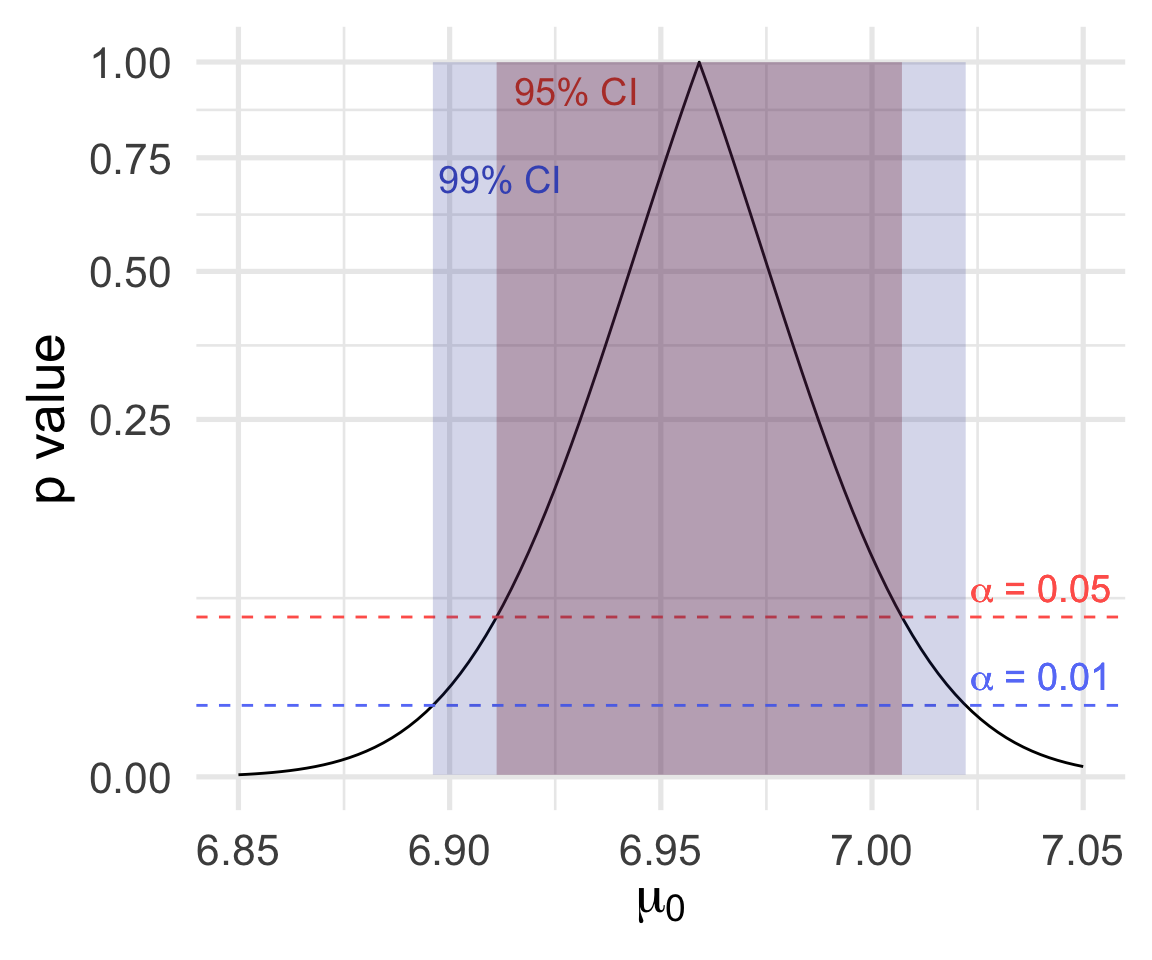
Left, \(p\)-values for a sequence of tests:
In other words:
\[\text{level $\alpha$ test rejects} \Longleftrightarrow \text{$1 - \alpha$ CI excludes}\]
t.test(...) functionSince tests and intervals go together, there is a single R function that computes both.
You have to make the decision using the \(p\) value:
Take a moment to locate each component of the test and estimates from the output.
Does the average U.S. adult sleep less than 7 hours?
This example leads to a lower-sided alternative:
\[ \begin{cases} H_0: &\mu = 7 \\ H_A: &\mu < 7 \end{cases} \]
The test statistic is the same as before:
\[ T = \frac{\bar{x} - 7}{SE(\bar{x})} = -1.671 \]
The lower-sided \(p\)-value is 0.0474:

For the \(p\)-value, we look at how often \(T\) is larger in the direction of the alternative.
Does the average U.S. adult sleep more than 7 hours?*
Now the alternative is in the opposite direction:
\[ \begin{cases} H_0: &\mu = 7 \\ H_A: &\mu > 7 \end{cases} \]
The test statistic is the same as before:
\[ T = \frac{\bar{x} - 7}{SE(\bar{x})} = -1.671 \]
The upper-sided \(p\)-value is 0.9526:
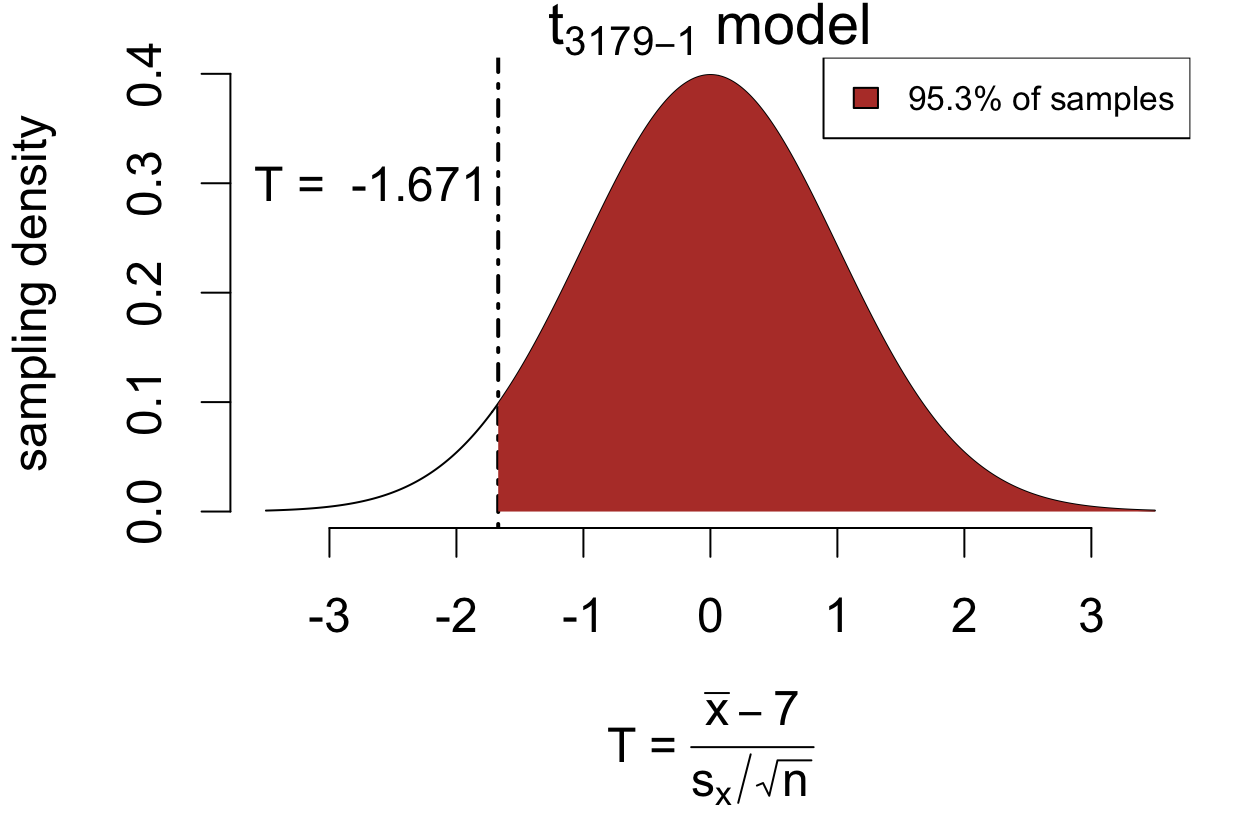
For the \(p\)-value, we look at how often \(T\) is larger in the direction of the alternative.
Tests for the mean can involve directional or non-directional alternatives. We refer to these as one-sided and two-sided tests, respectively.
| Test type | Alternative | Direction favoring alternative |
|---|---|---|
| Upper-sided | \(\mu > \mu_0\) | larger \(T\) |
| Lower-sided | \(\mu < \mu_0\) | smaller \(T\) |
| Two-sided | \(\mu \neq \mu_0\) | larger \(|T|\) |
The direction of the test affects the \(p\)-value calculation (and thus decision), but won’t change the test statistic.
Conceptually tricky, but easy in R:
Do U.S. adults sleep 7 hours per night?
Do U.S. adults sleep less than 7 hours per night?
Do U.S. adults sleep more than 7 hours per night?
Why don’t the tests agree?
One Sample t-test
data: sleep
t = -1.671, df = 3178, p-value = 0.09482
alternative hypothesis: true mean is not equal to 7
95 percent confidence interval:
6.911123 7.007090
sample estimates:
mean of x
6.959107
One Sample t-test
data: sleep
t = -1.671, df = 3178, p-value = 0.04741
alternative hypothesis: true mean is less than 7
95 percent confidence interval:
-Inf 6.999372
sample estimates:
mean of x
6.959107 The tests don’t agree if the same significance level is used.
Consider: a type I error occurs in each case if…
Using level \(\alpha = 0.05\) for both tests means that falsely inferring \(\mu < 7\) occurs:
So test (B) is more sensitive to data suggesting \(\mu < 7\) because it permits errors at a higher rate.
The following are 15 measurements of the pesticide DDT in kale in parts per million (ppm).
2.79, 2.93, 3.22, 3.78, 3.22, 3.38, 3.18, 3.33, 3.34, 3.06, 3.07, 3.56, 3.08, 4.64 and 3.34
C. E. Finsterwalder (1976) Collaborative study of an extension of the Mills et al method for the determination of pesticide residues in food. J. Off. Anal. Chem. 59, 169–171.
Imagine the target level for safety considerations is 3ppm or less, and you want to use this data to determine whether the mean DDT level is within safe limits.
\[ \begin{cases} H_0: &\mu = 3 \quad(\text{null hypothesis})\\ H_A: &\mu > 3 \quad(\text{alternative hypothesis}) \end{cases} \]
We choose this direction because we’re concerned with evidence that mean DDT exceeds the threshold.
If in fact \(\mu = 3\), then according to the \(t\) model 0.58% of samples would produce an error of this magnitude or more in the direction of the alternative:
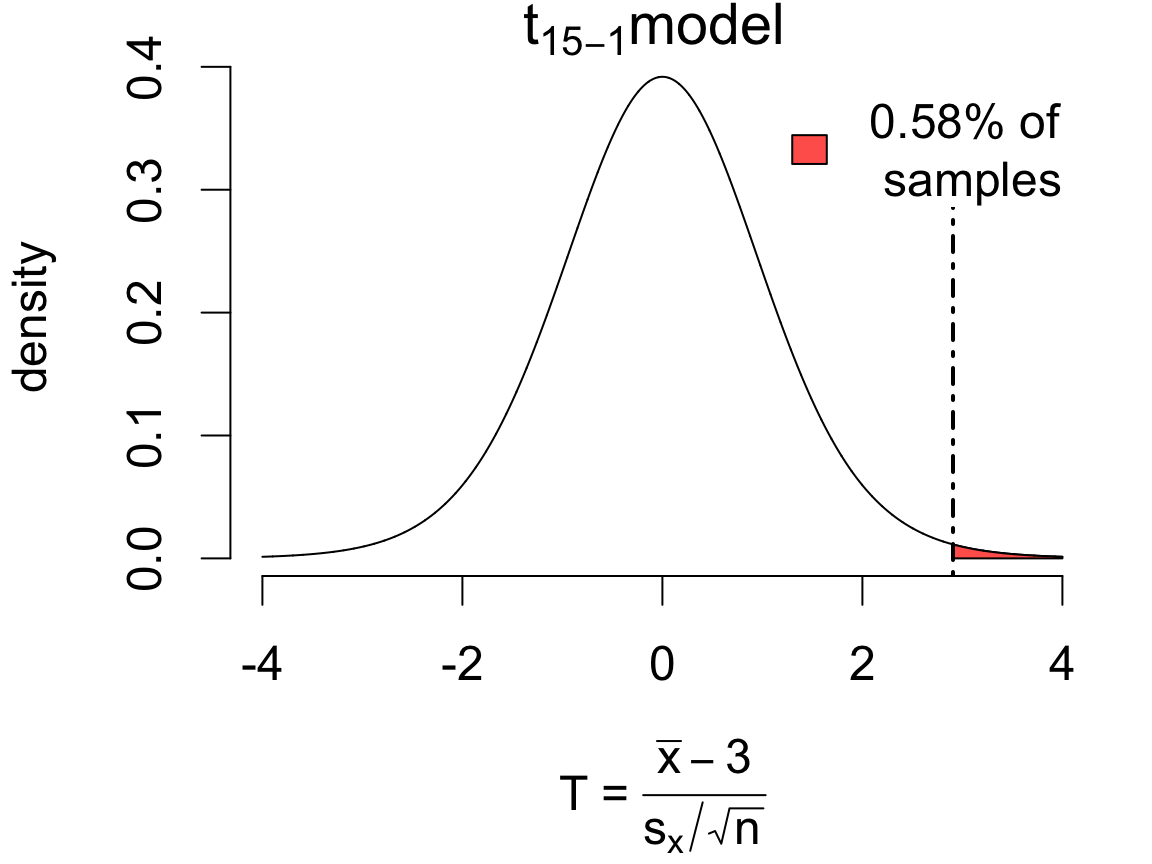
One Sample t-test
data: ddt
t = 2.9059, df = 14, p-value = 0.005753
alternative hypothesis: true mean is greater than 3
95 percent confidence interval:
3.129197 Inf
sample estimates:
mean of x
3.328 The data provide strong evidence that mean DDT in kale exceeds 3ppm (T = 2.9059 on 14 degrees of freedom, p = 0.0058). With 95% confidence, the mean DDT is estimated to be at least 3.129, with a point estimate of 3.32 (SE: 0.1129).
Notice the one-sided interval! (Inf = \(\infty\).) This is called a “lower confidence bound”.
Does the average U.S. adult wish to lose weight?
| subject | actual | desired | difference |
|---|---|---|---|
| 1 | 265 | 225 | 40 |
| 2 | 150 | 150 | 0 |
| 3 | 137 | 150 | -13 |
| 4 | 159 | 125 | 34 |
| 5 | 145 | 125 | 20 |
One Sample t-test
data: weight.diffs
t = 4.2172, df = 59, p-value = 4.311e-05
alternative hypothesis: true mean is greater than 0
95 percent confidence interval:
10.99824 Inf
sample estimates:
mean of x
18.21667 The data provide evidence that the average U.S. adult’s actual weight exceeds their desired weight (T = 4.2172 on 59 degrees of freedom, p < 0.0001).
Inference here is on the mean difference: \(H_0: \delta = 0\) vs. \(H_A: \delta > 0\).
Can we also do inference on a difference in means?
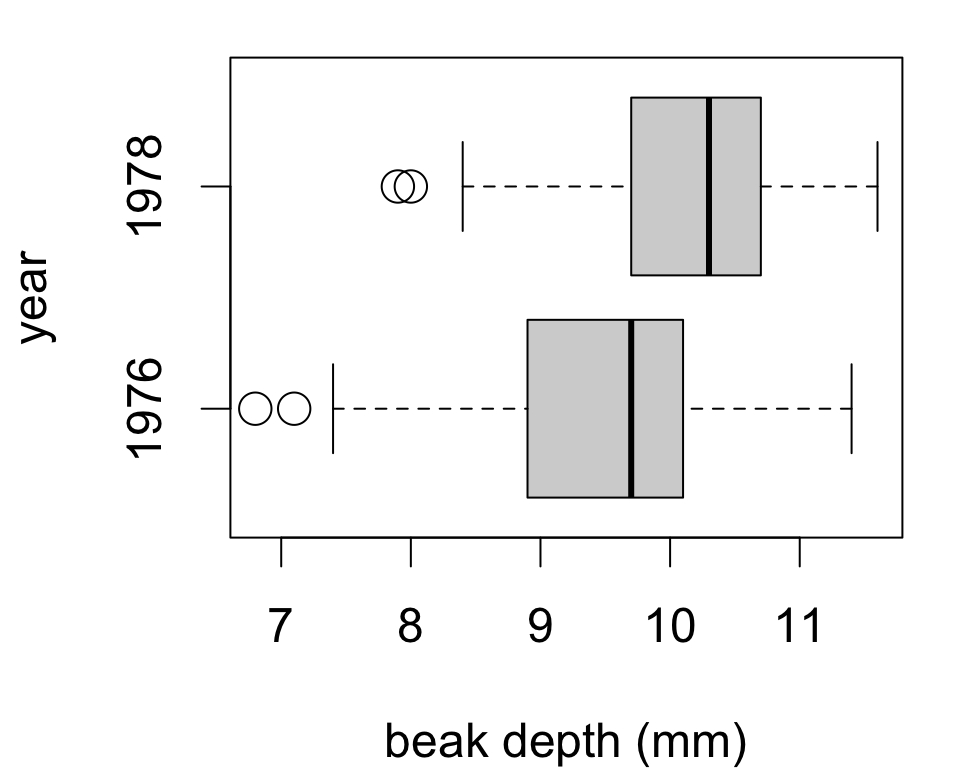
Peter and Rosemary Grant caught and measured birds from more than 20 generations of finches on Daphne Major.
severe drought in 1977 limited food to large tough seeds
selection pressure favoring larger and stronger beaks
hypothesis: beak depth increased in 1978 relative to 1976
| year | depth |
|---|---|
| 1976 | 10.8 |
| 1976 | 7.4 |
| 1978 | 11.4 |
| 1978 | 10.6 |
To answer this, we need to test a hypothesis involving two means:
\[ \begin{cases} H_0: &\mu_{1976} = \mu_{1978} \\ H_A: &\mu_{1976} < \mu_{1978} \end{cases} \]
If \(x_1, \dots, x_{58}\) are the 1976 observations and \(y_1, \dots, y_{65}\) are the 1978 observations:
Inference uses a new \(T\) statistic:
\[ T = \frac{(\bar{x} - \bar{y}) - \delta_0}{SE(\bar{x} - \bar{y})} \]
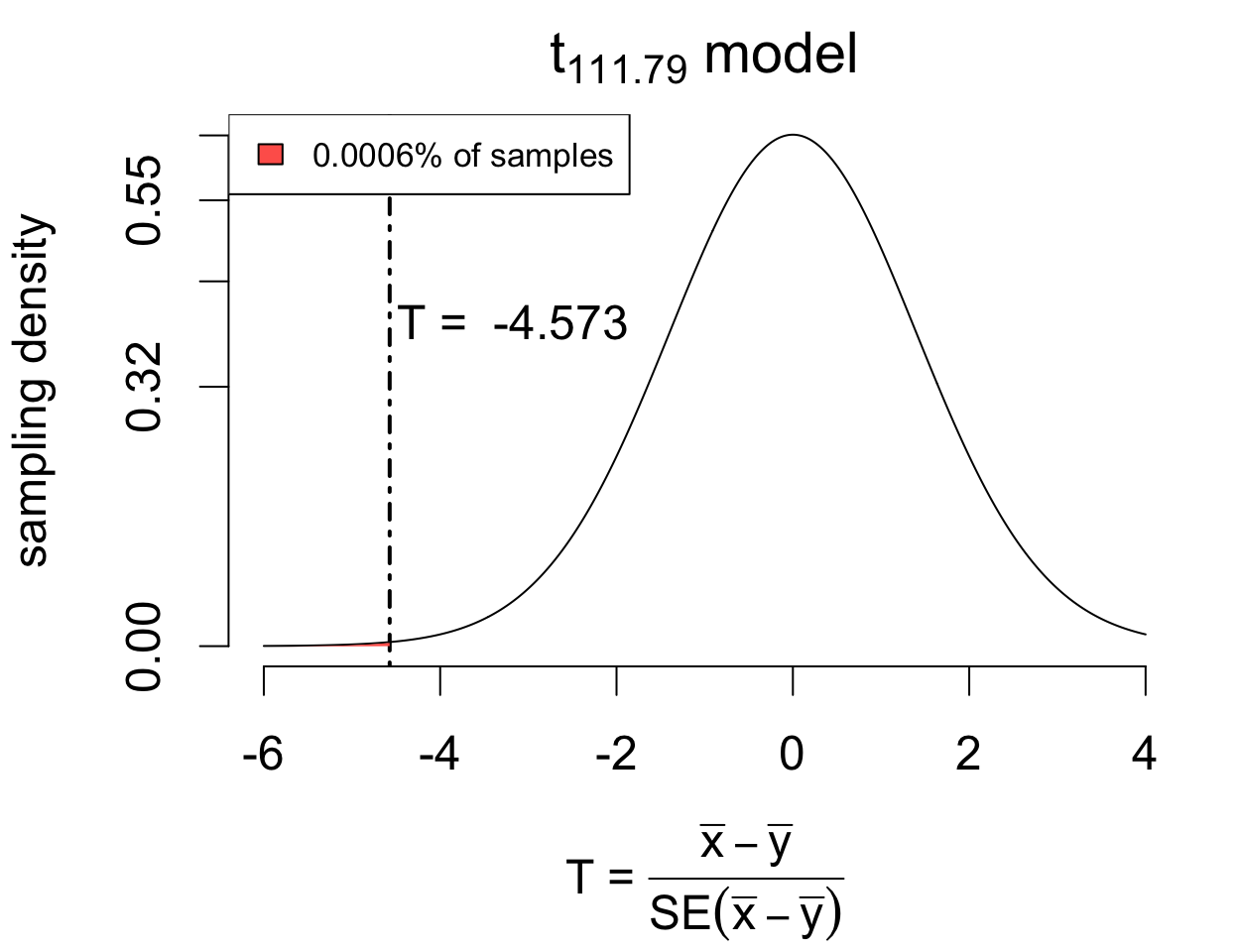
| year | depth.mean | depth.sd | n |
|---|---|---|---|
| 1976 | 9.453 | 0.9625 | 58 |
| 1978 | 10.19 | 0.8073 | 65 |
Point estimates: \[ \begin{align*} \bar{x} &= \qquad\qquad\qquad\qquad\\ \bar{y} &= \\ SE(\bar{x}) &= \\ SE(\bar{y}) &= \end{align*} \] Hypotheses: \[ \begin{cases} H_0: &\mu_{1976} - \mu_{1978} = 0 \\ H_A: &\mu_{1976} - \mu_{1978} < 0 \end{cases} \]
Test statistic: \[ \begin{align*} \bar{x} - \bar{y} &= \qquad\qquad\qquad\qquad\qquad\qquad\\ SE(\bar{x} - \bar{y}) &= \sqrt{SE(\bar{x})^2 + SE(\bar{y})^2} = \\ T &= \frac{(\bar{x} - \bar{y}) - \delta_0}{SE(\bar{x} - \bar{y})} = \end{align*} \] Conclusion: [reject]/[fail to reject] \(H_0\) in favor of \(H_A\)
How can you tell without the exact \(p\) value?
Welch Two Sample t-test
data: depth by year
t = -4.5727, df = 111.79, p-value = 6.255e-06
alternative hypothesis: true difference in means between group 1976 and group 1978 is less than 0
95 percent confidence interval:
-Inf -0.4698812
sample estimates:
mean in group 1976 mean in group 1978
9.453448 10.190769 The data provide evidence that mean beak depth increased following the drought (T = -4.5727 on 111.79 degrees of freedom, p < 0.0001). With 95% confidence, the mean increase is estimated to be at least 0.4699 mm, with a point estimate of 0.7373 (SE 0.1612).
Highly similar to the one-sample \(t\)-test, but notice:
depth ~ year (“depth depends on year”) and data frame finchmu now indicates hypothesized difference in means \(\delta_0\)The two-sample test is appropriate whenever two one-sample tests would be.
In other words, the test assumes that both samples are either:
To check, simply inspect each histogram.

The two-sample test is appropriate whenever two one-sample tests would be.
In other words, the test assumes that both samples are either:
Could also check side-by-side boxplots for:
This is also a nice visualization of differences between samples.
Does seeding clouds with silver iodide increase mean rainfall?
Data are rainfall measurements in a target area from 26 days when clouds were seeded and 26 days when clouds were not seeded.
rainfall gives volume of rainfall in acre-feettreatment indicates whether clouds were seededHypotheses to test: \[ \begin{cases} H_0: &\mu_\text{seeded} = \mu_\text{unseeded} \\ H_A: &\mu_\text{seeded} > \mu_\text{unseeded} \end{cases} \]
| rainfall | treatment |
|---|---|
| 334.1 | seeded |
| 489.1 | seeded |
| 200.7 | seeded |
| 40.6 | seeded |
| 21.7 | unseeded |
| 17.3 | unseeded |
| 68.5 | unseeded |
| 830.1 | unseeded |
Does seeding clouds with silver iodide increase mean rainfall?
Welch Two Sample t-test
data: rainfall by treatment
t = 1.9982, df = 33.855, p-value = 0.9731
alternative hypothesis: true difference in means between group seeded and group unseeded is less than 0
95 percent confidence interval:
-Inf 512.1582
sample estimates:
mean in group seeded mean in group unseeded
441.9846 164.5885
Welch Two Sample t-test
data: rainfall by treatment
t = 1.9982, df = 33.855, p-value = 0.02689
alternative hypothesis: true difference in means between group seeded and group unseeded is greater than 0
95 percent confidence interval:
42.63408 Inf
sample estimates:
mean in group seeded mean in group unseeded
441.9846 164.5885 You can tell which group R considers first based on which estimate is printed first.
'greater' is interpreted as [FIRST GROUP] > [SECOND GROUP]'less' is interpreted as [FIRST GROUP] < [SECOND GROUP]Does seeding clouds with silver iodide increase mean rainfall?
Welch Two Sample t-test
data: rainfall by treatment
t = 1.9982, df = 33.855, p-value = 0.02689
alternative hypothesis: true difference in means between group seeded and group unseeded is greater than 0
95 percent confidence interval:
42.63408 Inf
sample estimates:
mean in group seeded mean in group unseeded
441.9846 164.5885 The data provide evidence that cloud seeding increases mean rainfall (T = 1.9982 on 33.855 degrees of freedom, p = 0.02689). With 95% confidence, seeding is estimated to increase mean rainfall by at least 42.63 acre-feet, with a point estimate of 277.4 (SE 138.8199).
If it is reasonable to assume the (population) standard deviations are the same in each group, one can gain a bit of power by using a different standard error:
\[SE_\text{pooled}(\bar{x} - \bar{y}) = \sqrt{\frac{\color{red}{s_p^2}}{n_x} + \frac{\color{red}{s_p^2}}{n_y}} \quad\text{where}\quad \color{red}{s_p} = \underbrace{\sqrt{\frac{(n_x - 1)s_x^2 + (n_y - 1)s_y^2}{n_x + n_y - 2}}}_{\text{weighted average of } s_x^2 \;\&\; s_y^2}\]
Implement by adding var.equal = T as an argument to t.test().
A \(p\)-value captures how often you’d make a mistake if \(H_0\) were true.
Welch Two Sample t-test
data: rainfall by treatment
t = 1.9982, df = 33.855, p-value = 0.02689
alternative hypothesis: true difference in means between group seeded and group unseeded is greater than 0
95 percent confidence interval:
42.63408 Inf
sample estimates:
mean in group seeded mean in group unseeded
441.9846 164.5885 If there is no effect of cloud seeding, then we would see \(T > 1.9982\) for 2.69% of samples.
While unlikely, our sample could have been among that 2.69%
By rejecting here we are willing to be wrong 2.69% of the time
But you can also make a mistake when \(H_0\) is false!
Welch Two Sample t-test
data: rainfall by treatment
t = 1.9982, df = 33.855, p-value = 0.02689
alternative hypothesis: true difference in means between group seeded and group unseeded is greater than 0
95 percent confidence interval:
42.63408 Inf
sample estimates:
mean in group seeded mean in group unseeded
441.9846 164.5885 Suppose we test at the 1% level.
The test fails to reject (\(p > 0.01\)), but that doesn’t completely rule out \(H_A\).
The estimated effect – an increase of 277.4 acre-feet – could be too small relative to the variability in rainfall.
Summary stats for cloud data:
| treatment | mean | sd | n |
|---|---|---|---|
| seeded | 442 | 650.8 | 26 |
| unseeded | 164.6 | 278.4 | 26 |
We can approximate the type II error rate by:
If in fact the effect size is exactly 277, a level 1% test with similar data will fail to reject 80.3% of the time!
Summary stats for cloud data:
| treatment | mean | sd | n |
|---|---|---|---|
| seeded | 442 | 650.8 | 26 |
| unseeded | 164.6 | 278.4 | 26 |
Type II error rate depends on effect size:
If in fact the effect size is exactly 400, a level 1% test with similar data will fail to reject 57.9% of the time.
Summary stats for cloud data:
| treatment | mean | sd | n |
|---|---|---|---|
| seeded | 442 | 650.8 | 26 |
| unseeded | 164.6 | 278.4 | 26 |
Type II error rate depends on effect size:
If in fact the effect size is exactly 100, a level 1% test with similar data will fail to reject 96.3% of the time.
The power of a test refers to its true rejection rate under an alternative and is defined as: \[\beta = \underbrace{(1 - \text{type II error rate})}_\text{correct decision rate when alternative is true}\]
Power is often interpreted as a detection rate:
Power depends on the exact alternative scenario:
Power is usually represented as a curve depending on the true difference.
Power curves for the test applied to the cloud data:
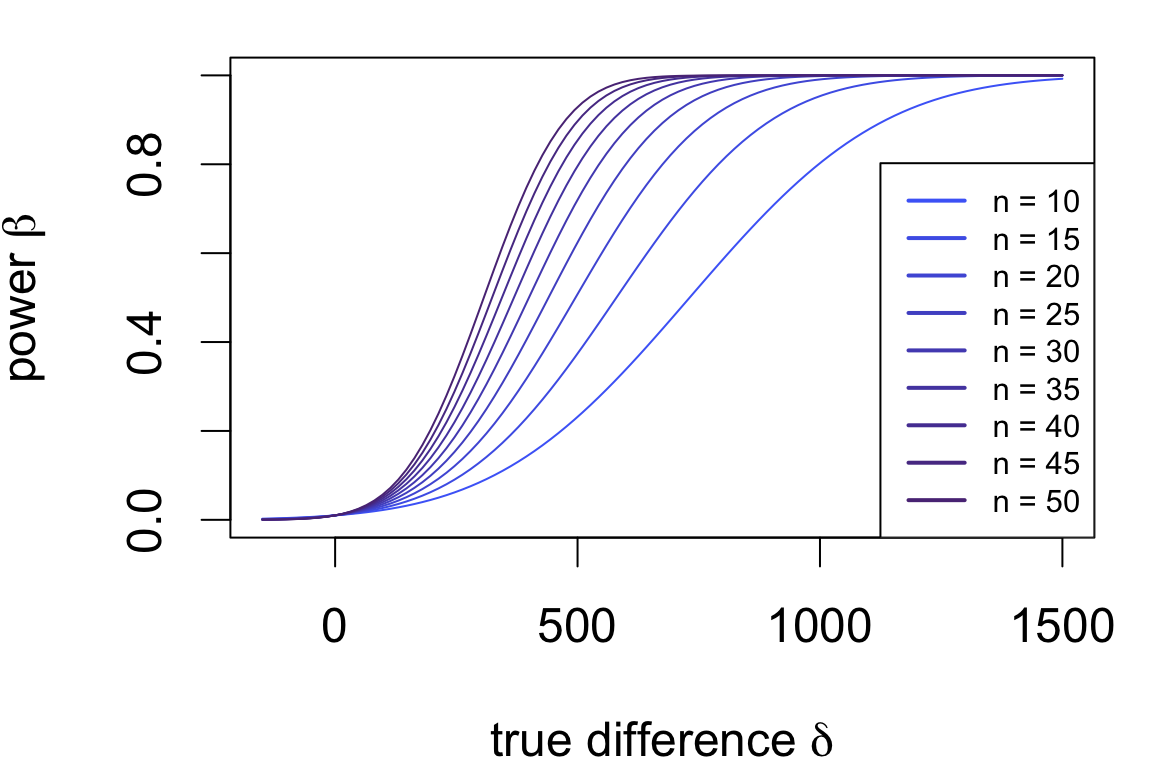
Assumptions:
Which sample size achieves a specific \(\beta, \delta\)?
If you were (re)designing the study, how much data should you collect to detect a specified effect size?
To detect a difference of 250 or more due to cloud seeding with power 0.9:
power.t.test(power = 0.9, # target power level
delta = 250, # smallest difference
sd = 650, # largest population SD
sig.level = 0.01,
type = 'two.sample',
alternative = 'one.sided')
Two-sample t test power calculation
n = 177.349
delta = 250
sd = 650
sig.level = 0.01
power = 0.9
alternative = one.sided
NOTE: n is number in *each* groupFor a conservative estimate, use:
\(\Longrightarrow\) we need at least 177 observations in each group to detect a difference of 250 or more at least 90% of the time
Does mean body temperature differ between men and women?
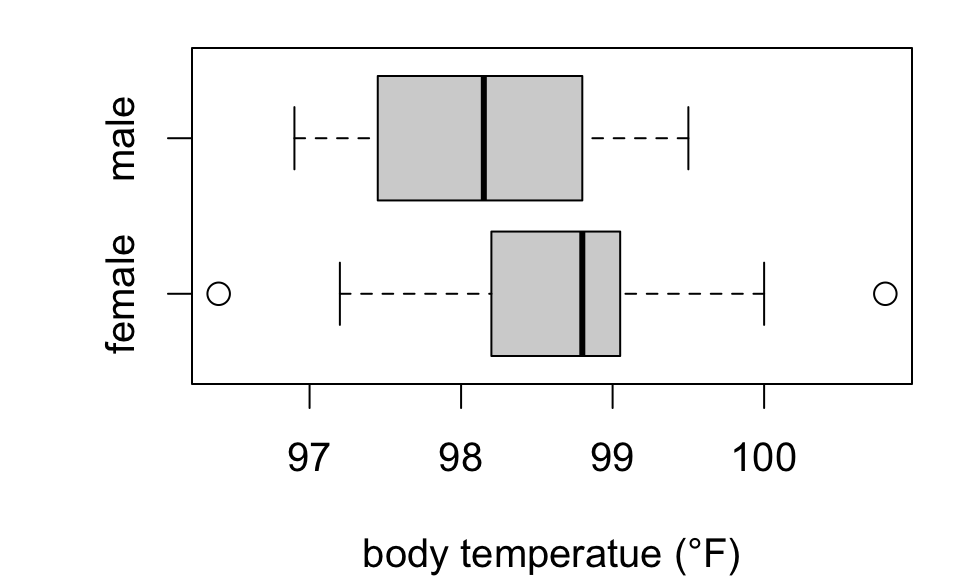
Test \(H_0: \mu_F = \mu_M\) against \(H_A: \mu_F \neq \mu_M\)
Welch Two Sample t-test
data: body.temp by sex
t = 1.7118, df = 34.329, p-value = 0.09595
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
-0.09204497 1.07783444
sample estimates:
mean in group female mean in group male
98.65789 98.16500 Suggestive but insufficient evidence that mean body temperature differs by sex.
Notice: estimated difference (F - M) is 0.493 °F (SE 0.2879)
Here are estimates from two larger samples of 65 individuals each (compared with 19, 20):
| sex | mean.temp | se | n |
|---|---|---|---|
| female | 98.39 | 0.09222 | 65 |
| male | 98.1 | 0.08667 | 65 |
Welch Two Sample t-test
data: body.temp by sex
t = 2.2854, df = 127.51, p-value = 0.02394
alternative hypothesis: true difference in means between group female and group male is not equal to 0
95 percent confidence interval:
0.03881298 0.53964856
sample estimates:
mean in group female mean in group male
98.39385 98.10462 The data provide evidence that mean body temperature differs by sex (T = 2.29 on 127.51 degrees of freedom, p = 0.02394).
If you collect enough data, you can detect an arbitrarily small difference in means.
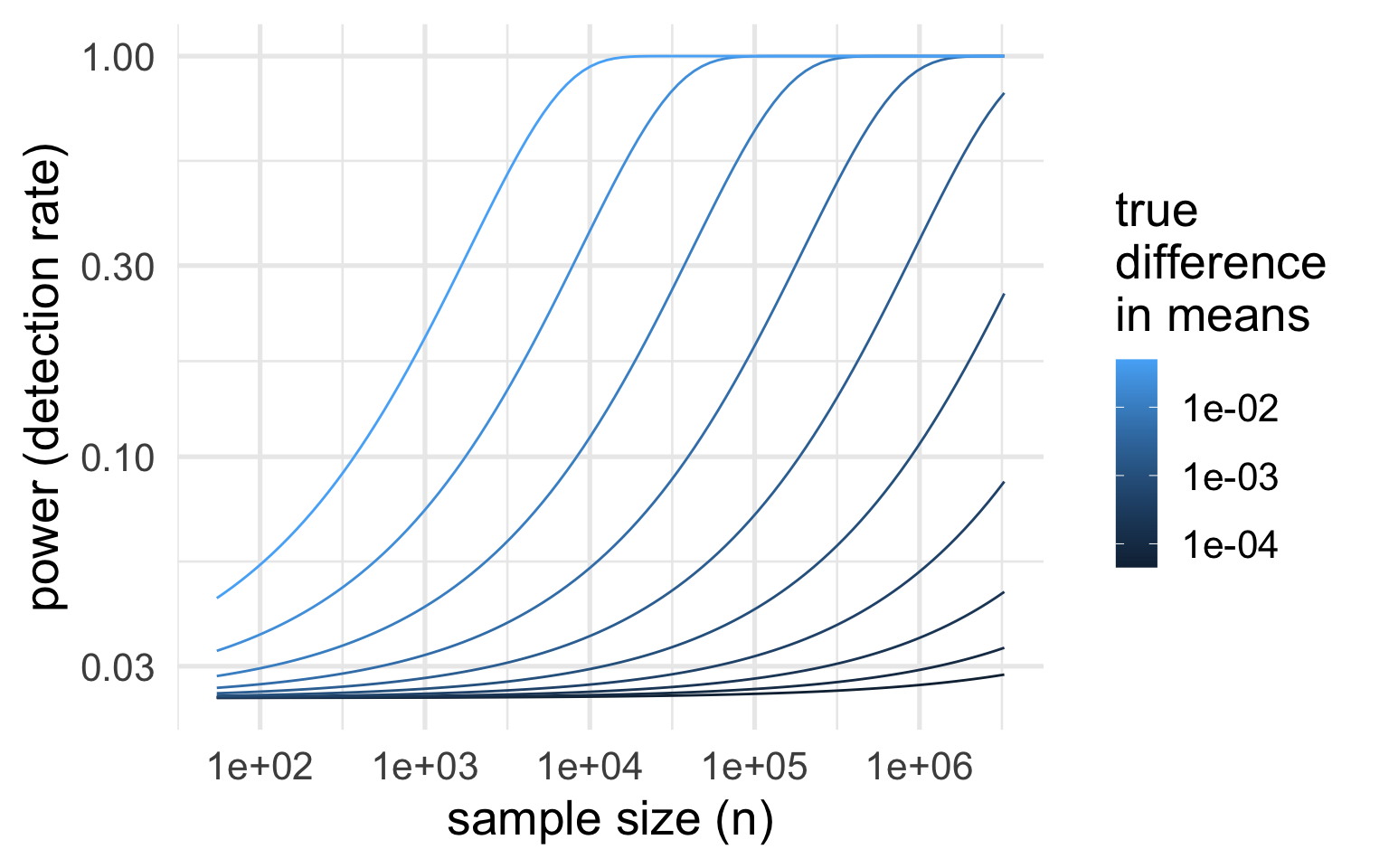
So keep in mind:
It’s a good idea to always check your point estimates and ask whether findings are practically meaningful.
Chick weights at 20 days of age by diet:
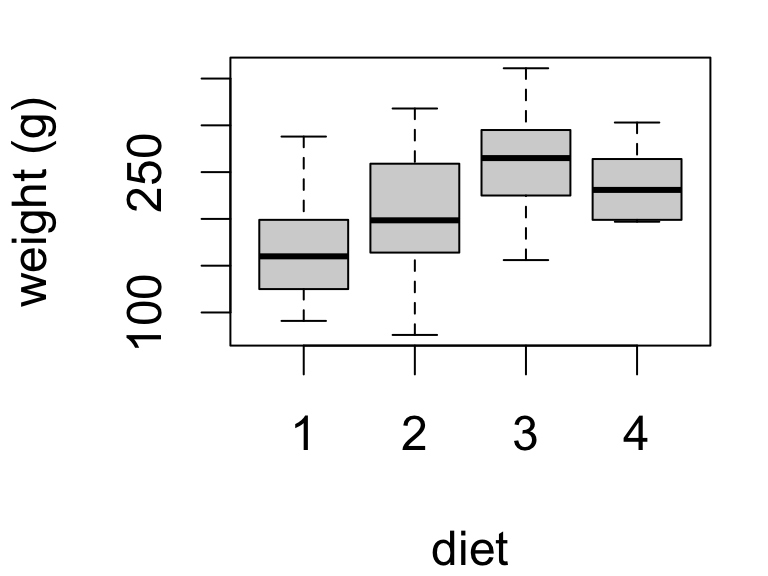
Here we have four means to compare.
| diet | mean | se | sd | n |
|---|---|---|---|---|
| 1 | 170.4 | 13.45 | 55.44 | 17 |
| 2 | 205.6 | 22.22 | 70.25 | 10 |
| 3 | 258.9 | 20.63 | 65.24 | 10 |
| 4 | 233.9 | 12.52 | 37.57 | 9 |
This is experimental data: chicks were randomly allocated one of the four diets.
Let \(\mu_i = \text{mean weight on diet } i = 1, 2, 3, 4\).
The hypothesis that there are no differences in means by diet is:
\[ H_0: \mu_1 = \mu_2 = \mu_3 = \mu_4 \quad (\text{no difference in means}) \]
The alternative, if this is false, is that there is at least one difference:
\[ H_A: \mu_i \neq \mu_j \;\text{for some}\; i \neq j\quad (\text{at least one difference}) \]
This is known as an “omnibus” test because of the composite alternative.
Here are two made-up examples of the same four sample means with different SEs.
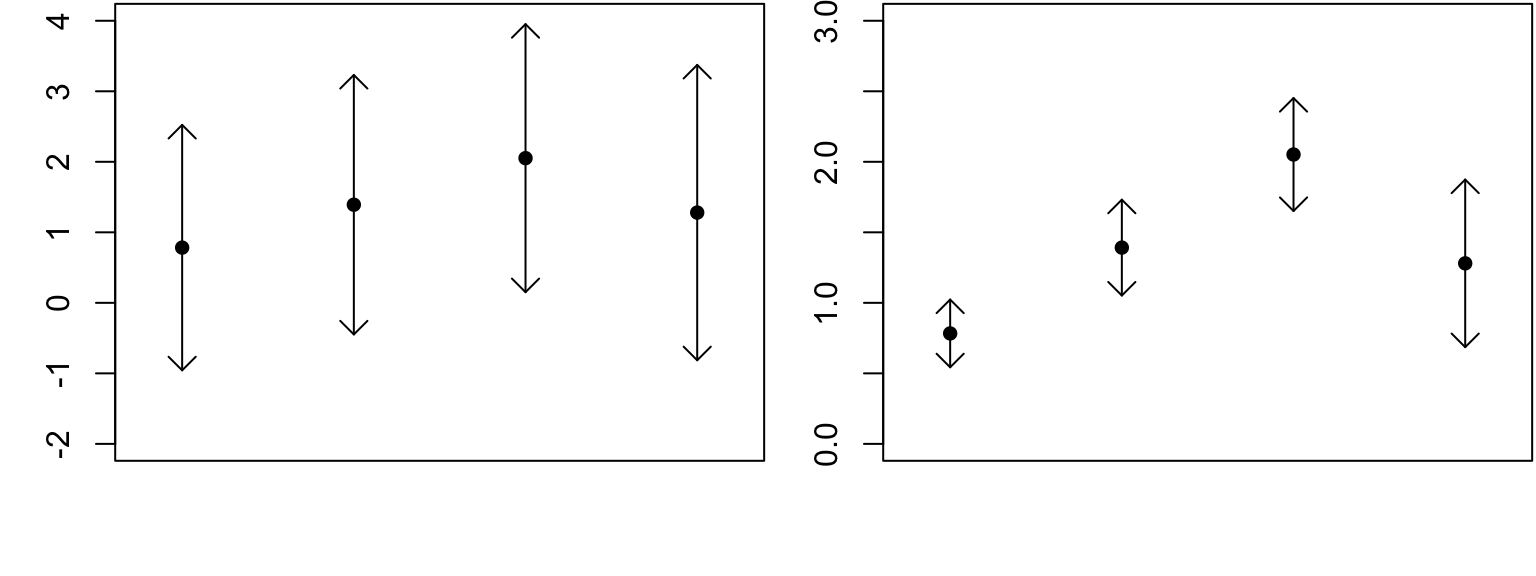
Why does it look like there’s a difference at right but not at left?
Think about the \(t\)-test: we say there’s a difference if \(T = \frac{\text{estimate} - \text{hypothesis}}{\text{variability}}\) is large.
Same idea here: we see differences if they are big relative to the variability in estimates.
Partitioning variation into two or more components is called “analysis of variance”
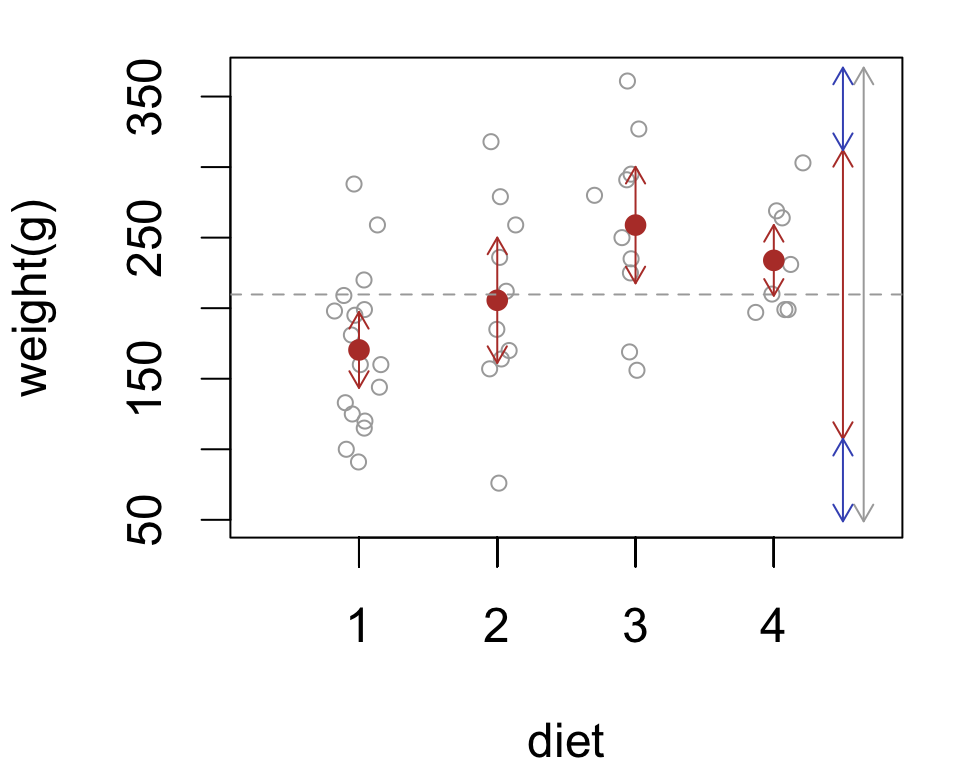
For the chick data, two sources of variability:
group variability between diets
error variability among chicks
The analysis of variance (ANOVA) model:
\[\color{grey}{\text{total variation}} = \color{red}{\text{group variation}} + \color{blue}{\text{error variation}}\]
We’ll base the test on the ratio \(F = \frac{\color{red}{\text{group variation}}}{\color{blue}{\text{error variation}}}\) and reject \(H_0\) if the ratio is large enough.
The \(F\) statistic measures variability attributable to group differences relative to variability attributable to individual differences.
Notation:
Measures of variability:
\[\color{red}{MSG} = \frac{1}{k - 1}\sum_i n_i(\bar{x}_i - \bar{x})^2 \quad(\color{red}{\text{group}})\] \[\color{blue}{MSE} = \frac{1}{n - k}\sum_i (n_i - 1)s_i^2 \quad(\color{blue}{\text{error}})\] Ratio:
\[F = \frac{\color{red}{MSG}}{\color{blue}{MSE}} \quad\left(\frac{\color{red}{\text{group variation}}}{\color{blue}{\text{error variation}}}\right)\]
Provided that
the \(F\) statistic has a sampling distribution well-approximated by an \(F_{k - 1, n - k}\) model.
To test the hypotheses:
\[ \begin{cases} H_0: &\mu_1 = \mu_2 = \mu_3 = \mu_4 \\ H_A: &\mu_i \neq \mu_j \quad\text{for some}\quad i \neq j \end{cases} \] Calculate the \(F\) statistic:
# ingredients of mean squares
k <- nrow(chicks.summary)
n <- nrow(chicks)
n.i <- chicks.summary$n
xbar.i <- chicks.summary$mean
s.i <- chicks.summary$sd
xbar <- mean(chicks$weight)
# mean squares
msg <- sum(n.i*(xbar.i - xbar)^2)/(k - 1)
mse <- sum((n.i - 1)*s.i^2)/(n - k)
# f statistic
fstat <- msg/mse
fstat[1] 5.463598And reject \(H_0\) when \(F\) is large.
\[ \begin{cases} H_0: &\mu_1 = \mu_2 = \mu_3 = \mu_4 \\ H_A: &\mu_i \neq \mu_j \quad\text{for some}\quad i \neq j \end{cases} \]
\(F = \frac{\color{red}{\text{group variation}}}{\color{blue}{\text{error variation}}} = \frac{MSG}{MSE} = 5.4636\).
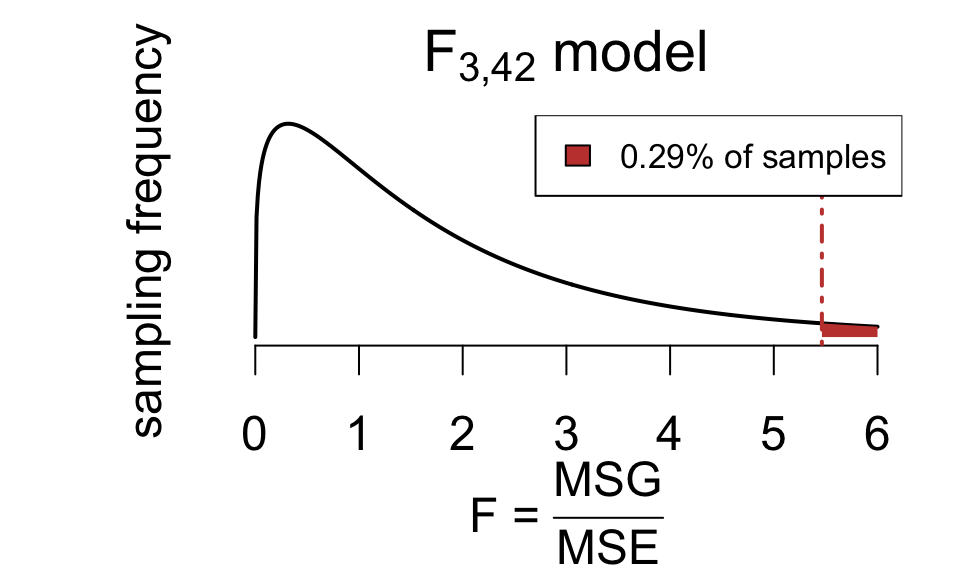
F = 5.4636 means the variation in weight attributable to diets is 5.46 times greater than individual variation among chicks.
The \(p\)-value for the test is 0.0029:
if there is truly no difference in means, then under 1% of samples (about 2 in 1000) would produce at least as much diet-to-diet variability as we observed
so in this case we reject \(H_0\) at the 1% level
The aov(...) function fits ANOVA models using a formula/dataframe specification:
| Df | Sum Sq | Mean Sq | F value | Pr(>F) | |
|---|---|---|---|---|---|
| diet | 3 | 55881 | 18627 | 5.464 | 0.002909 |
| Residuals | 42 | 143190 | 3409 | NA | NA |
Conventional interpretation style closely follows that of previous inferences for one or two means:
The data provide evidence of an effect of diet on mean weight (F = 5.464 on 3 and 42 df, p = 0.0029).
The results of an analysis of variance are traditionally displayed in a table.
| Source | degrees of freedom | Sum of squares | Mean square | F statistic | p-value |
|---|---|---|---|---|---|
| Group | \(k - 1\) | SSG | \(MSG = \frac{SSG}{k - 1}\) | \(\frac{MSG}{MSE}\) | \(P(F > F_\text{obs})\) |
| Error | \(n - k\) | SSE | \(MSE = \frac{SSE}{n - k}\) |
Formally, the ANOVA model says \[(n - 1)S^2 = SSG + SSE\]
| Source | DF | Sum sq. | Mean sq. | F statistic | p-value |
|---|---|---|---|---|---|
| Group | \(k - 1\) | SSG | \(MSG = \frac{SSG}{k - 1}\) | \(\frac{MSG}{MSE}\) | \(P(F > F_\text{obs})\) |
| Error | \(n - k\) | SSE | \(MSE = \frac{SSE}{n - k}\) |
Here is what the fitted model looks like in R:
Call:
aov(formula = weight ~ diet, data = chicks)
Terms:
diet Residuals
Sum of Squares 55881.02 143190.31
Deg. of Freedom 3 42
Residual standard error: 58.38915
Estimated effects may be unbalancedExercise: compute MSE, MSG, and F based on this output.
Rules of thumb for level \(\alpha = 0.05\) tests:
A common measure of effect size is \[\eta^2 = \frac{SSG}{SST} \quad\left(\frac{\text{group variation}}{\text{total variation}}\right)\] where \[SST = SSG + SSE = (n - 1)S^2_x\] This is the proportion of total variation attributed to the grouping factor.
# Effect Size for ANOVA (Type I)
Parameter | Eta2 | 95% CI
-------------------------------
diet | 0.28 | [0.08, 1.00]
- One-sided CIs: upper bound fixed at [1.00].An estimated 28% of variation in weight is attributable to diet.
The confidence interval is for the population analogue of \(\eta^2\).
How many chicks should we measure to detect an average group difference of 20g?
Group variation on the order of 20g amounts to about (since \(n_i\) varies) \[SSG \approx (k - 1)(n_i\times400) \approx 14400\] which is an effect size of \[\eta^2 = \frac{14400}{143190 + 14400} = 0.0914\] i.e., group variation is around 9.14% of total variation.
To power the study to detect \(\eta^2 = 0.1\) use the approximation (assumes \(k \ll n\)):
power.anova.test(groups = 4,
sig.level = 0.05,
power = 0.8,
between.var = 0.1, # eta^2
within.var = 0.9) # 1 - eta^2
Balanced one-way analysis of variance power calculation
groups = 4
n = 33.70068
between.var = 0.1
within.var = 0.9
sig.level = 0.05
power = 0.8
NOTE: n is number in each groupWe’d need 34 chicks per group.
From data on lifespans of lab mice fed calorie-restricted diets:
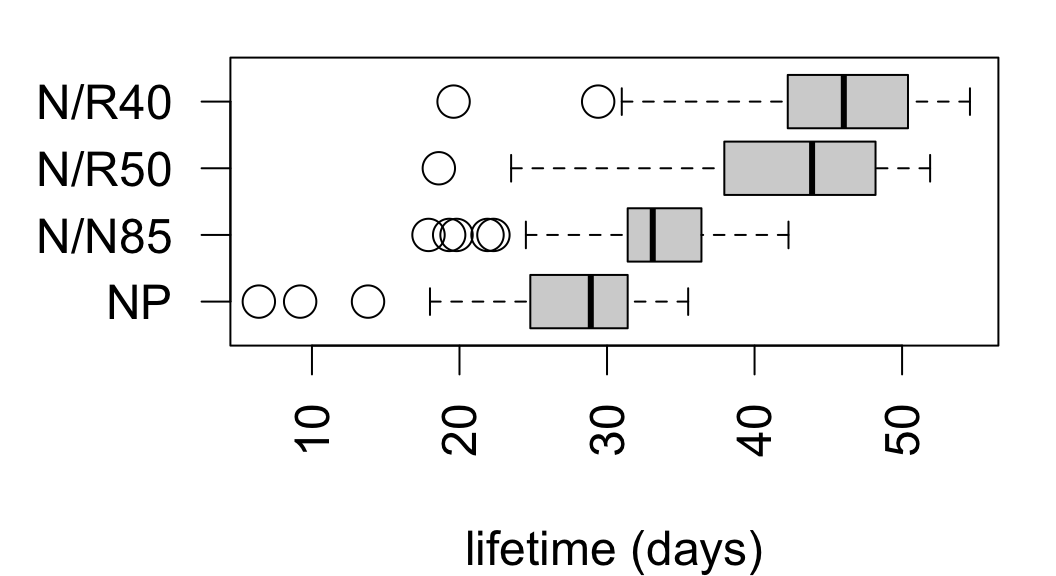
| diet | mean | sd | n |
|---|---|---|---|
| NP | 27.4 | 6.134 | 49 |
| N/N85 | 32.69 | 5.125 | 57 |
| N/R50 | 42.3 | 7.768 | 71 |
| N/R40 | 45.12 | 6.703 | 60 |
ANOVA omnibus test:
\[ \begin{align*} &H_0: \mu_\text{NP} = \mu_\text{N/N85} = \mu_\text{N/R50} = \mu_\text{N/R40} \\ &H_A: \text{at least two means differ} \end{align*} \]
Df Sum Sq Mean Sq F value Pr(>F)
diet 3 11426 3809 87.41 <2e-16 ***
Residuals 233 10152 44
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The data provide evidence that diet restriction has an effect on mean lifetime among mice (F = 87.41 on 3 and 233 degrees of freedom, p < 0.0001).
From data on weight change among 72 young anorexic women after a period of therapy:

| treat | post - pre | sd | n |
|---|---|---|---|
| ctrl | -0.45 | 7.989 | 26 |
| cbt | 3.007 | 7.309 | 29 |
| ft | 7.265 | 7.157 | 17 |
ANOVA omnibus test: \[ \begin{align*} &H_0: \mu_\text{ctrl} = \mu_\text{cbt} = \mu_\text{ft} \\ &H_A: \text{at least two means differ} \end{align*} \]
Df Sum Sq Mean Sq F value Pr(>F)
treat 2 615 307.32 5.422 0.0065 **
Residuals 69 3911 56.68
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1The data provide evidence of an effect of therapy on mean weight change among young women with anorexia (F = 5.422 on 2 and 69 degrees of freedom, p = 0.0065).
\[ \begin{align*} &H_0: \mu_\text{NP} = \mu_\text{N/N85} = \mu_\text{N/R50} = \mu_\text{N/R40} \\ &H_A: \text{at least two means differ} \end{align*} \]

Df Sum Sq Mean Sq F value Pr(>F)
diet 3 11426 3809 87.41 <2e-16 ***
Residuals 233 10152 44
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Effect Size for ANOVA (Type I)
Parameter | Eta2 | 95% CI
-------------------------------
diet | 0.53 | [0.44, 0.60]The data provide evidence that caloric restriction affects mean lifespan (F = 87.41 on 3 and 233 degrees of freedom, p < 0.0001). With 95% confidence, an estimated 44%-60% of variability in lifespans is attributable to caloric intake.
The ANOVA tells us there’s evidence that caloric intake affects mean lifespan. So now that we’ve inferred an effect, we might want to know:
We can answer these questions with post-hoc (after-the-fact) inferences on:
Interval estimates for group means in ANOVA are similar to marginal confidence intervals except for two details.
| diet | estimate | SE | 95% CI |
|---|---|---|---|
| NP | 27.4 | 0.943 | (25.54, 29.26) |
| N/N85 | 32.69 | 0.8743 | (30.97, 34.41) |
| N/R50 | 42.3 | 0.7834 | (40.75, 43.84) |
| N/R40 | 45.12 | 0.8522 | (43.44, 46.8) |
\[SE_i = \frac{s_\text{pooled}}{\sqrt{n_i}} = \frac{\sqrt{MSE}}{\sqrt{n_i}}\]
Rationale:
For multiple intervals we can distinguish two types of coverage.
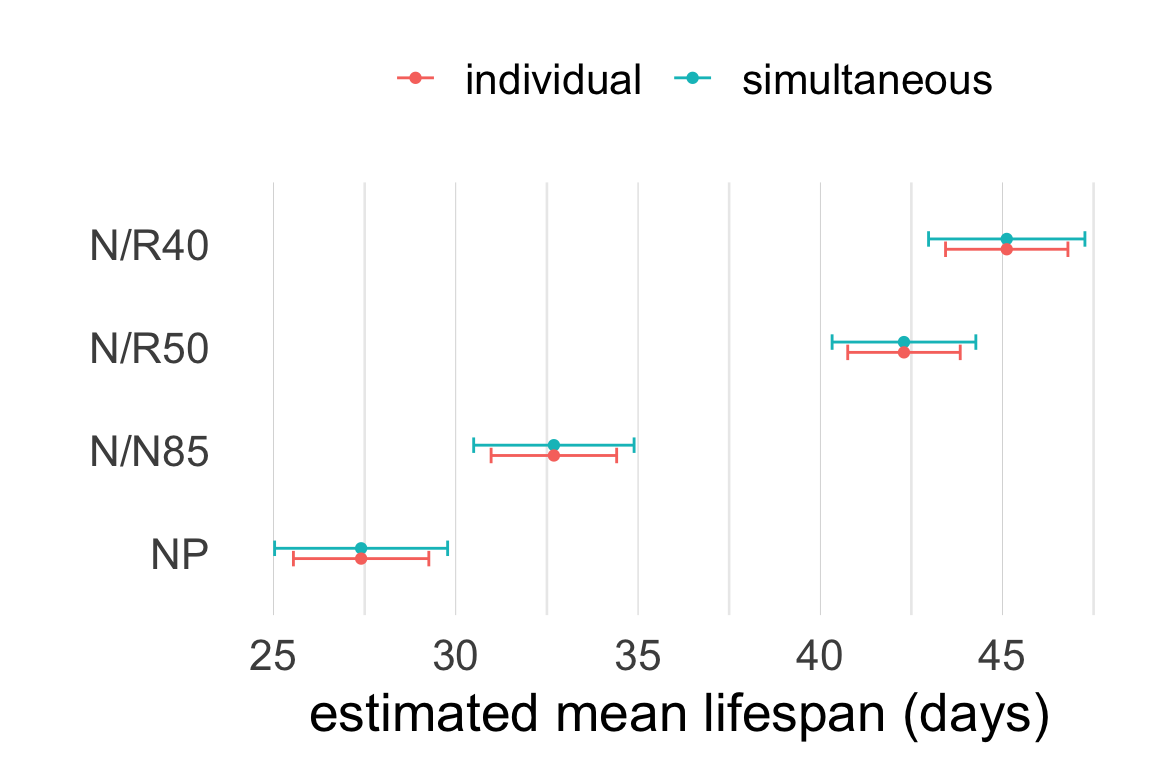
The Bonferroni correction for \(k\) intervals consists in changing the individual coverage level to \(\left(1 - \frac{\alpha}{k}\right)\%\).
diet emmean SE df lower.CL upper.CL
NP 27.4 0.943 233 25.0 29.8
N/N85 32.7 0.874 233 30.5 34.9
N/R50 42.3 0.783 233 40.3 44.3
N/R40 45.1 0.852 233 43.0 47.3
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 4 estimates Caution: these intervals do NOT indicate which means differ significantly.
The difference \(\mu_{NP} - \mu_{N/N85}\) is an example of a “contrast” involving two means.
Simultaneous inference on pairwise contrasts will determine which means differ and by how much.
| difference | estimate | SE |
|---|---|---|
| NP - (N/N85) | -5.289 | 1.286 |
| NP - (N/R50) | -14.9 | 1.226 |
| NP - (N/R40) | -17.71 | 1.271 |
| (N/N85) - (N/R50) | -9.606 | 1.174 |
| (N/N85) - (N/R40) | -12.43 | 1.221 |
| (N/R50) - (N/R40) | -2.819 | 1.158 |
Remarks:
point estimates are \(\bar{x}_i - \bar{x}_j\)
\(SE_{ij} = SE(\bar{x}_i - \bar{x}_j) = s_\text{pooled}\sqrt{\frac{1}{n_i} + \frac{1}{n_j}}\)
inference is based on a \(t_{n - k}\) model
Multiplicity corrections must adjust for the number of contrasts (6), not means (4).
Which means differ significantly?
emmeans then contrast then test:
contrast estimate SE df t.ratio p.value
NP - (N/N85) -5.29 1.29 233 -4.113 0.0003
NP - (N/R50) -14.90 1.23 233 -12.150 <.0001
NP - (N/R40) -17.71 1.27 233 -13.938 <.0001
(N/N85) - (N/R50) -9.61 1.17 233 -8.183 <.0001
(N/N85) - (N/R40) -12.43 1.22 233 -10.177 <.0001
(N/R50) - (N/R40) -2.82 1.16 233 -2.436 0.0937
P value adjustment: bonferroni method for 6 tests Hypotheses for pairwise tests:
\[\begin{cases} H_0: \mu_i - \mu_j = 0 \\ H_A: \mu_i - \mu_j \neq 0 \end{cases}\] Test statistic:
\[T_{ij} = \frac{\bar{x}_i - \bar{x}_j}{SE_{ij}}\]
\(p\)-values are obtained from a \(t_{n - k}\) model for the sampling distribution of \(T_{ij}\).
Which means differ significantly?
emmeans then contrast then test:
contrast estimate SE df t.ratio p.value
NP - (N/N85) -5.29 1.29 233 -4.113 0.0003
NP - (N/R50) -14.90 1.23 233 -12.150 <.0001
NP - (N/R40) -17.71 1.27 233 -13.938 <.0001
(N/N85) - (N/R50) -9.61 1.17 233 -8.183 <.0001
(N/N85) - (N/R40) -12.43 1.22 233 -10.177 <.0001
(N/R50) - (N/R40) -2.82 1.16 233 -2.436 0.0937
P value adjustment: bonferroni method for 6 tests The data provide evidence at the 5% significance level that mean lifespan differs among all levels of diet restriction except the N/R40 and N/R50 groups (p = 0.0937), for which the evidence is suggestive but inconclusive.
Using unadjusted \(p\)-values will inflate type I error rates.
setting adjust = 'none':
contrast estimate SE df t.ratio p.value
NP - (N/N85) -5.29 1.29 233 -4.113 0.0001
NP - (N/R50) -14.90 1.23 233 -12.150 <.0001
NP - (N/R40) -17.71 1.27 233 -13.938 <.0001
(N/N85) - (N/R50) -9.61 1.17 233 -8.183 <.0001
(N/N85) - (N/R40) -12.43 1.22 233 -10.177 <.0001
(N/R50) - (N/R40) -2.82 1.16 233 -2.436 0.0156Failure to adjust for multiple inferences leads to a different conclusion:
The data provide evidence at the 5% significance levelthat mean lifespan differs among all levels of diet restriction.
This is incorrect, because the joint significance level is not 5%.
Without adjustment, type I error could be as high as \(k\times\alpha = 6\times 0.05 = 0.3\).
How much do means differ?
emmeans then contrast then confint:
emmeans(object = fit, specs = ~ diet) |>
contrast('pairwise') |>
confint(level = 0.95, adjust = 'bonferroni') contrast estimate SE df lower.CL upper.CL
NP - (N/N85) -5.29 1.29 233 -8.71 -1.867
NP - (N/R50) -14.90 1.23 233 -18.16 -11.633
NP - (N/R40) -17.71 1.27 233 -21.10 -14.333
(N/N85) - (N/R50) -9.61 1.17 233 -12.73 -6.482
(N/N85) - (N/R40) -12.43 1.22 233 -15.67 -9.177
(N/R50) - (N/R40) -2.82 1.16 233 -5.90 0.261
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 6 estimates level specifies joint coverage after adjustmentIntervals are for the contrast \(\mu_i - \mu_j\):
\[\bar{x}_i - \bar{x}_j \pm c\times SE_{ij}\]
The critical value \(c\) is obtained from the \(t_{n - k}\) model.
For a \((1 - \alpha)\times 100\%\) confidence interval with Bonferroni correction:
\[c = \left(1 - \frac{\alpha}{2k}\right) \;\text{quantile}\]
How much do means differ?
emmeans then contrast then confint:
emmeans(object = fit, specs = ~ diet) |>
contrast('pairwise') |>
confint(level = 0.95, adjust = 'bonferroni') contrast estimate SE df lower.CL upper.CL
NP - (N/N85) -5.29 1.29 233 -8.71 -1.867
NP - (N/R50) -14.90 1.23 233 -18.16 -11.633
NP - (N/R40) -17.71 1.27 233 -21.10 -14.333
(N/N85) - (N/R50) -9.61 1.17 233 -12.73 -6.482
(N/N85) - (N/R40) -12.43 1.22 233 -15.67 -9.177
(N/R50) - (N/R40) -2.82 1.16 233 -5.90 0.261
Confidence level used: 0.95
Conf-level adjustment: bonferroni method for 6 estimates Interpretations are the same as usual:
With 95% confidence, mean lifespan on a normal diet is estimated to exceed mean lifespan on an unrestricted diet by between 1.87 and 8.71 days, with a point estimate of 5.29 days difference (SE 1.29).
Another option is to visualize the pairwise comparison inferences by displaying simultaneous 95% intervals.
Easy to spot significant contrasts:
Does diet restriction increase mean lifespan, and if so by how much?
Specify contrast('trt.vs.ctrl'):
| contrast | estimate | SE | 95% CI |
|---|---|---|---|
| (N/N85) - NP | 5.289 | 1.286 | (2.23, 8.34) |
| (N/R50) - NP | 14.9 | 1.226 | (11.98, 17.81) |
| (N/R40) - NP | 17.71 | 1.271 | (14.7, 20.73) |
Multiple inference adjustment uses Dunnett’s method
adjust = 'dunnett'Comparisons will be relative to first group or factor level in R
With 95% confidence, relative to an unrestricted diet…
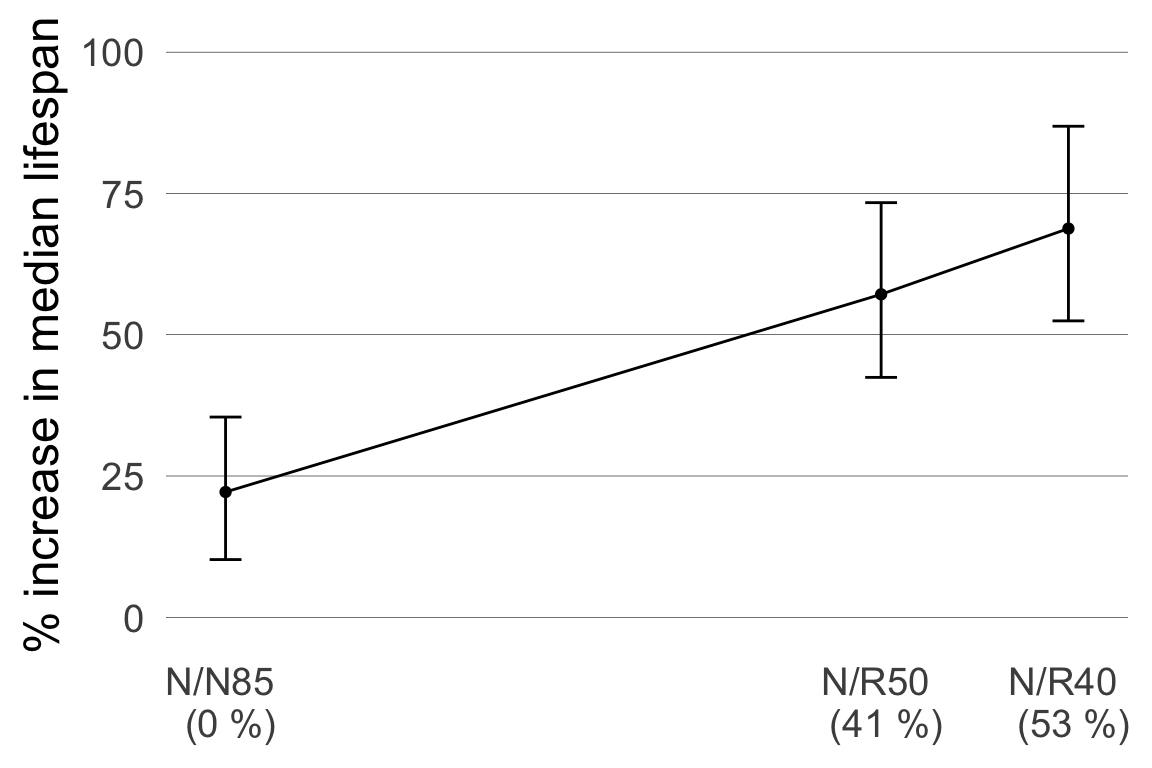
Can we instead estimate a percent change in lifespan relative to the control?
The contrast in log-lifetimes would be:
\[ \log(\mu_{N85}) - \log(\mu_{NP}) = \log\left(\frac{\mu_{N85}}{\mu_{NP}}\right) \] So to answer the question:
| contrast | estimate | 95% CI |
|---|---|---|
| (N/R50)/NP | 1.572 | (1.42, 1.73) |
| (N/R40)/NP | 1.688 | (1.52, 1.87) |
Fact: mean log lifetime = log median lifetime.
With 95% confidence, diet restriction to 40kcal (a 52.9% reduction relative to an 85kCal diet) is estimated to increase median lifespan in mice by 52% to 87%.
Extra credit: work out and interpret the interval estimate for the contrast not shown above.
We can use the log-contrasts to estimate a response curve relating caloric reduction and change in median lifespan.
Simplifying heuristics:
The inferences we’ve developed so far are based on simple statistical models:
Both models assume underlying data distributions are described by…
We call these called parametric methods.
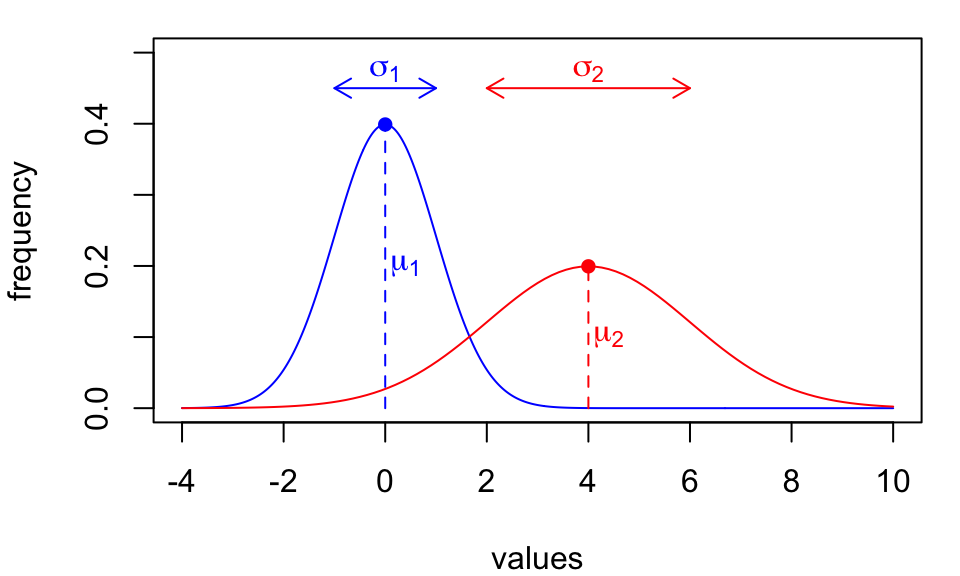
Parametric model assumptions don’t always hold.
DDT concentrations (ppm) in kale samples.

With only \(n = 12\) observations, it’s hard to assess the shape of the distribution.
Serum cholesterol (mg/L) on two diets.

The distribution for the oat bran group is right-skewed with an outlier to the left.
| ddt | sign |
|---|---|
| 2.79 | - |
| 2.93 | - |
| 3.08 | + |
| 3.18 | + |
| 3.22 | + |
| 3.22 | + |
| 3.33 | + |
| 3.34 | + |
| 3.34 | + |
| 3.38 | + |
| 3.56 | + |
| 3.78 | + |
Consider the following hypothesis and alternative:
\[ \begin{cases} H_0: &m = 3 \qquad(\text{median is } 3 \text{ppm})\\ H_A: &m > 3 \qquad(\text{median exceeds } 3 \text{ppm}) \end{cases} \]
If \(m = 3\) you’d expect 3ppm to evenly divide the data.
But actually 10 observations (83%) are larger and 2 observations (17%) are smaller; using combinatorics, this occurs by chance only 1.9% of the time.
The data provide evidence that median DDT in kale exceeds 3ppm (p = 0.019).
This is called a sign test, and it is nonparametric because it makes no assumptions about the underlying distribution.
| ddt | di |
|---|---|
| 2.79 | -0.21 |
| 2.93 | -0.07 |
| 3.08 | 0.08 |
| 3.18 | 0.18 |
| 3.22 | 0.22 |
| 3.22 | 0.22 |
| 3.33 | 0.33 |
| 3.34 | 0.34 |
| 3.34 | 0.34 |
| 3.38 | 0.38 |
| 3.56 | 0.56 |
| 3.78 | 0.78 |
Now consider:
\[ \begin{cases} H_0: &c = 3 \qquad(\text{center is } 3 \text{ppm})\\ H_A: &c > 3 \qquad(\text{center exceeds } 3 \text{ppm}) \end{cases} \] If the distribution is symmetric, deviations from center should be about the same in either direction.
The signed rank test leverages this expectation:
If \(V\) is large, there is more spread to the right of \(c_0\), providing evidence favoring \(H_A\).
| ddt | di | rank | sign | vi |
|---|---|---|---|---|
| 2.93 | -0.07 | 1 | -1 | -1 |
| 3.08 | 0.08 | 2 | 1 | 2 |
| 3.18 | 0.18 | 3 | 1 | 3 |
| 2.79 | -0.21 | 4 | -1 | -4 |
| 3.22 | 0.22 | 5.5 | 1 | 5.5 |
| 3.22 | 0.22 | 5.5 | 1 | 5.5 |
| 3.33 | 0.33 | 7 | 1 | 7 |
| 3.34 | 0.34 | 8.5 | 1 | 8.5 |
| 3.34 | 0.34 | 8.5 | 1 | 8.5 |
| 3.38 | 0.38 | 10 | 1 | 10 |
| 3.56 | 0.56 | 11 | 1 | 11 |
| 3.78 | 0.78 | 12 | 1 | 12 |
Signed rank statistic: \[ \begin{align*} V &= 2+3+5.5+5.5+7+8.5+8.5+10+11+12 \\ &= 73 \end{align*} \]
There are 4096 possible sign combinations; of these, only about 0.43% give a larger value of \(V\).
Wilcoxon signed rank test with continuity correction
data: ddt
V = 73, p-value = 0.004269
alternative hypothesis: true location is greater than 3The data provide evidence that the center of the distribution of DDT in kale exceeds 3ppm (signed rank test, p = 0.00427).
| bp | diet |
|---|---|
| 0 | FishOil |
| 12 | FishOil |
| 10 | FishOil |
| 2 | FishOil |
| 14 | FishOil |
| 8 | FishOil |
| -3 | RegularOil |
| -4 | RegularOil |
| -6 | RegularOil |
| 0 | RegularOil |
| 1 | RegularOil |
| 2 | RegularOil |
Consider using data on blood pressure percent reduction to test: \[ \begin{cases} H_0: &c_F = c_R \qquad(\text{no effect})\\ H_A: &c_F > c_R \qquad(\text{fish oil produces greater reduction}) \end{cases} \]
If there is no effect of diet, ranks will be randomly distributed among groups. This idea leads to the rank sum test:
\[W = \text{rank sum} - \frac{n_1(n_1 + 1)}{2}\]
When \(W\) is near \(0\) or \(\frac{n(n + 1)}{2} - \frac{n_1(n_1 + 1)}{2}\) there is more separation.
| bp | diet | rank |
|---|---|---|
| -6 | RegularOil | 1 |
| -4 | RegularOil | 2 |
| -3 | RegularOil | 3 |
| 0 | FishOil | 4.5 |
| 0 | RegularOil | 4.5 |
| 1 | RegularOil | 6 |
| 2 | FishOil | 7.5 |
| 2 | RegularOil | 7.5 |
| 8 | FishOil | 9 |
| 10 | FishOil | 10 |
| 12 | FishOil | 11 |
| 14 | FishOil | 12 |
Rank sum statistic:
\[ W = \underbrace{(4.5+7.5+9+10+11+12)}_\text{rank sum} - \underbrace{\frac{6\times 7}{2}}_\text{adjustment} = 54 - 21 = 33 \] There are 924 ways to allocate ranks to groups; among these, larger values of \(W\) occur about 0.99% of the time.
Wilcoxon rank sum test with continuity correction
data: bp by diet
W = 33, p-value = 0.009903
alternative hypothesis: true location shift is greater than 0The data provide evidence that fish oil reduces blood pressure by more than regular oil (rank sum test, p = 0.0099).
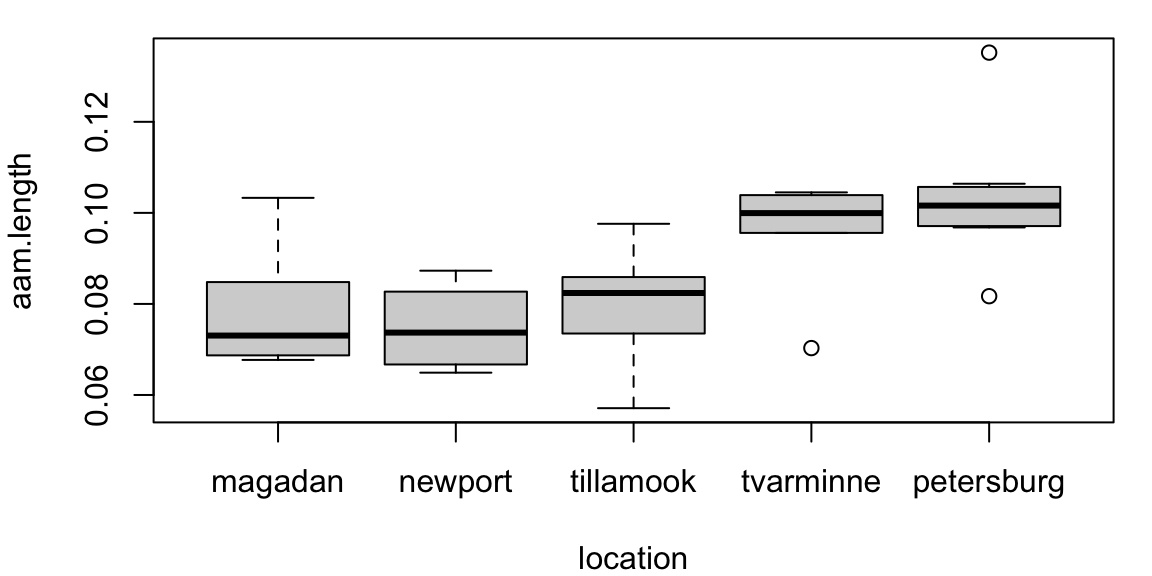
Here assumptions may not hold:
\[ \begin{cases} H_0: &c_M = c_N = c_{Ti} = c_{Tv} = c_P \\ H_A: &c_i \neq c_j \quad\text{ for some }\quad i\neq j \end{cases} \]
An ANOVA-like test can be formulated using ranks of pooled observations:
\[ U = \frac{\sum_{j = 1}^k n_j (\bar{r}_j - \bar{r})^2}{\sum_{i = 1}^n (r_i - \bar{r})^2} \qquad \left(\frac{\text{group variation}}{\text{total variation}}\right) \]
If there are location differences, \(U\) will be large.
Omnibus test for location differences:
Kruskal-Wallis rank sum test
data: aam.length by location
Kruskal-Wallis chi-squared = 16.405, df = 4, p-value = 0.002521Post-hoc comparisions use pairwise rank sum tests:
Pairwise comparisons using Wilcoxon rank sum exact test
data: mussels$aam.length and mussels$location
magadan newport tillamook tvarminne
newport 1.000 - - -
tillamook 1.000 1.000 - -
tvarminne 0.293 0.127 0.312 -
petersburg 0.059 0.022 0.084 1.000
P value adjustment method: bonferroni The data provide evidence that the distribution of AAM lengths differs by geographic location (Kruskal-Wallis test, p = 0.0025)
Pairwise comparisons indicate that distributions differ significantly between Petersburg and Newport populations (p = 0.022)
The omnibus test in ANOVA gives a similar result:
Df Sum Sq Mean Sq F value Pr(>F)
location 4 0.004520 0.0011299 7.121 0.000281 ***
Residuals 34 0.005395 0.0001587
---
Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1But the pairwise comparisons differ:
# A tibble: 4 × 6
contrast estimate SE df t.ratio p.value
<chr> <dbl> <dbl> <dbl> <dbl> <dbl>
1 magadan - petersburg -0.0254 0.00652 34 -3.90 0.00430
2 newport - tvarminne -0.0209 0.00680 34 -3.07 0.0417
3 newport - petersburg -0.0286 0.00652 34 -4.39 0.00103
4 tillamook - petersburg -0.0232 0.00621 34 -3.74 0.00670
The parametric test is more sensitive to skewness and outliers!
Two-sample and ANOVA-type rank-based inference procedures detect location shifts only.
While we write the hypotheses in terms of centers by convention, really we’re testing:
These tests are not sensitive to alternatives in which centers differ due to shape.
Nonparametric methods provide attractive alternatives to \(t\) and \(F\) tests when assumptions don’t hold or aren’t easily checked.
helpful for small sample sizes or odd data distributions
more robust to outliers
fewer assumptions
| No. of groups | Method | Test of… | Assumptions |
|---|---|---|---|
| One sample | Sign test | median | none |
| One sample | Signed rank test | center/location | symmetry |
| Two sample | Rank sum test | center/location | location shifts only |
| Many samples | Kruskal-Wallis test | center/location | location shifts only |
STAT218